数学啸寄巧
∫−∞+∞e−x2dx=π
∫0∞xne−axdx=an+1n!
- 经典积不出函数(一定要注意上下限是 ∞ 和 −∞ 还是 ∞ 和 0 ,取用不同的积分)(注意奇偶性)
∫0∞x2ne−ax2dx=2n+1an1⋅3⋅5⋯(2n−1)aπ
∫0∞e−λx2dx=21λπ
∫0∞xe−λx2dx=2λ1
∫0∞x2e−λx2dx=41λ3π
∫0∞x3e−λx2dx=2λ21
∫0∞x4e−λx2dx=83λ5π
∫0∞x5e−λx2dx=λ31
∫0∞x5e−λx2dx=1615λ7π
- 类似 cosxcos3x 一类的,使用积化和差公式之后再积分。
- 共轭运算的性质: z1z2=z1⋅z2
- sinx 和 cosx 用 e 指数表示
cosx=2eix+e−ix
sinx=2ieix−e−ix
- sinx 和 cosx 取共轭都是它本身
- 三角函数相关积分
∫xcosαxdx=∂α∂∫sinαxdx=−∂α∂α1cosαx=α21cosαx+αxsinαx
- ∇=∂x∂ (一维形式)
相对论基础
m=1−c2v2m0
E=m02c4+p2c2
同时, E=E0+EK ,其中 E0=m0c2
前量子力学
热辐射、黑体辐射、普朗�克的量子假说
热辐射
- 热辐射原理:表面分子受热振动辐射电磁波
- 温度高 → 动能大 → 辐射能量高 → 辐射电磁波的波长短
- 不仅与物体的温度有关,也与物体表面的性质有关
- 单色辐出度 Mλ :物体单位表面,单位时间内发出的波长在 λ 附近单位波长间隔内的的电磁波的能量。
Mλ(T)=dλdEλ
Mν(T)=dνdEν
- 辐出度 M(T) :物体在单位时间内从单位面积上发射的各种电磁波的总能量。(总辐出度:积分;单色辐出度的极值:求导)
M(T)=∫0∞Mλ(T)dλ
M(T)=∫0∞Mν(T)dν
- Mλ 与 Mν 的关系:由于 ν=λc ,代入积分可得:
Mλ(T)=λ2cMν(T)
- 要注意, Mλ 的表达式中不能出现 ν ,另一个同理。
- 吸收比:辐射从外界入射到物体表面时,吸收能量与入射能量之比。
α(T)=E入射E吸收
- 单色吸收比 α(λ,T) ,将能量改为在 λ 到 λ+dλ 波段的能量。
基尔霍夫定律
- 若干个不同的物体在绝热恒温体内经过热辐射交换能量达到平衡态,要维持温度不变,物体吸收的辐射能等于辐射出去的能量
- 辐出度较大的物体,吸收本领一定也较大,也即物体单色辐出度与单色吸收比的比值为波长和温度的普适函数。
α(λ,T)M(λ,T)=M0(λ,T)
黑体辐射
- 黑体:完全吸收各种波长电磁波而无反射的物体,是理想的发射体。
- 黑体辐射分布:
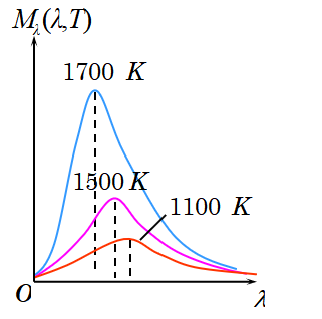
- 理解:温度越高,辐射的波长越短,这与图中结果相符。
- 斯特藩-玻尔兹曼定律 (斯特藩-玻尔兹曼常量: σ=5.67×10−8W⋅m−2⋅K−4 )
M(T)=σT4
(注意, M(T) 是单位时间,单位面积的辐出度)
- 维恩位移定律(极值波长 λm 与黑体温度 T 之积为常数 b=2.897×10−3m⋅K
λmT=b
- 不怎么精准的公式们
- 将黑体辐射看作一系列驻波,每一频率的驻波振动对应同频率的简谐振子振动 → 电磁波能量分布可以看作一系列频率的简谐振子的能量分布 → 谐振子的能量具有任意连续值
- 维恩公式: Mν(T)=αν3e−βν/T 高频区符合,长波区不符合
- 瑞利-金斯公式: Mv(T)=c22πν2kT 长波区符合,高频区不符合(趋向于正无穷)
- 普朗克经验公式:
Mν=c22πν2ehν/kT−1hν
- 普朗克公式的假设:原子振子振动的能量量子化
- Mν=c22πν2ϵˉ
- E=hν
- 普朗克常数: h=6.6260755×10−34J⋅s
- 代入上面积分的结论可以知道:Mλ=λ52πc2ehc/kλT−1h
- 与其他几个公式的关系
- 高频极限 → 维恩公式( ehν/T≫1 )
- 低频极限 → 瑞利-金斯公式(ehν/T≃1+kThν )
- 积分 → 斯特藩-玻尔兹曼定律
- 极值 → 维恩位移定律
- 做题:
- 艾里斑
- 艾里斑的公式![[大学物理#^c431b5]]
- 艾里斑占总能量的 84%
光电效应、光量子假说、康普顿效应
光电效应
- 电流强度随光电管两端电压的增加而增加
- 饱和电流与入射光强 I �成正比
- 遏止电压(反向电压达到遏止电压时,电流完全变为0)/光电子初动能与入射光频率成正比
- 光电子即时发射
- eUa=e(Kν−U0)
- 截距: A=eU0
- 斜率: h=eK
- 通过测定斜率可以确定普朗克常数
- 对于光子
- 能量 ϵ=hν=pc=λch=mc2
- 动量 p=chν=λh
- 一个黑体单位表面在单位时间内发出的总光子数:
dN=εdEν=hν1Mν(T)dν=c22πν2ekThν−11dν
N=∫0∞ c22πν2e br / kT−11dν =c2h32πk3T3∫0∞ex−1x2dx
ex−11=n=1∑∞e−nx
康普顿效应
- X 射线经过物质散射时,散射线的波长发生变化的现象
- 出现波长大于 λ0 的新散射波长 λ
- 波长差随散射角的增大而增大,与散射物质无关
- 原波长的谱线强度降低,新波长谱线强度增大
- 经典理论只能说明波长不变的散射(带电粒子受入射电磁波的作用发生受迫振动)
- 解释
- 与散射物质中束缚微弱的外层电子弹性碰撞,光子能量减少,波长变长
- 与物质中束缚很紧的内层电子发生碰撞,光子能量不会显著减少,出现波长相同的射线
- 计算:看作光子与静止的“自由电子”的弹性碰撞( m0=me )。示意图:
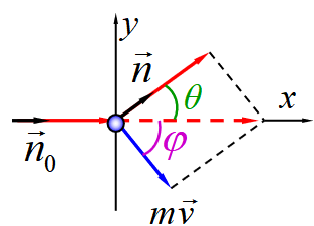
- 能量守恒: hν0+m0c2=hν+mc2
- 动量守恒:λ0hn0=λhn+mv
- x 方向 chν0=chνcosθ+mvcosφ
- y 方向 0=chνsinθ−mvsinφ
- 相对论条件: m=1−c2v2m0
- Δλ=λ−λ0=m0ch(1−cosθ)=2λcsin22θ
- θ=π 时, λ 最大
- 电子反冲动能:Ek=λ0ch−λ0+2λcch
- 电子动量: mv=λ0h+λ0+2λch
- 电子的康普顿波长:λc=mech=2.43×10−12 m
- 自由电子不可能吸收光子(否则速度达到光速),只能散射光子。
- 做题:
- 电子反冲动能 Ek=h∣Δν∣
- X 射线中也是光子
- 注意在康普顿散射中,光子散射后能量变少……(这里是倒数!当然从原理上也可以理解)
二者关系
- 同:单个光子和电子相互作用,能量守恒
- 异:
- 光电:束缚电子吸收光子,系统能量守恒,动量不守恒
- 康普顿:光子与自由电子的弹性碰撞,能量动量都守恒
氢原子光谱、玻尔理论、物质波
氢原子光谱与玻尔理论
- 原子光谱不是连续的而是线状的。
- 玻尔理论假设
- 电子绕核运动,有许多稳定的状态,每个定态对应电子的一个能级。
- 从高能量状态 En 跃迁到低能量状态 Em ,产生一个光子,频率: hν=En−Em
- 角动量量子化:电子绕核做圆周运动,角动量是量子化的 mevnrn=nℏ 其中 n 是整数。
- 约化普朗克常数 ℏ=2πh ,注意上面角动量那里是约化普朗克常数,但计算光子能量那里是普朗克常数
- 经典理论+波尔假设(圆周运动向心力式子+角动量量子化两式联立),可以得到氢原子的半径:
r=rn=n2πmee2ε0h2=n2r1n=1,2,⋯
r1=πmee2ε0h2=a0=0.053nm
E=21mev2−4πϵ0re2
其中,可以通过向心力那个公式求出氢原子的动能,之后可以求得:
E=−8πϵ0re2
代入氢原子的半径之后,可以得到:
E=En=−8πε0rne2=−8ε02h2n2mee4=n2E1n=1,2,⋯
其中,基态能为 E1=−13.6eV ,也称为电离能。
- 当我们考虑电子从高能级跃迁到低能级产生光子的过程的时候,可以通过下面的公式计算出光子的频率(其中 m 是较低的能级, n 是较高的能级)
ν=hEn−Em=hE1(n21−m21)=8ε02h3me4(m21−n21)
(注意上式中 E1 是负数,所以一个是 n21−m21 ,一个是 m21−n21 )
R=8ε02h3cmee4=1.097373×107 m−1
ν=cR(m21−n21)
- 对于核电荷为 Ze 的类氢离子,也可以用上面的思路联立方程求出:
- 向心力: F=4πϵ0r2Ze2
- 半径: rn=Zn2a0
- 能级: E=−8ϵ02h2n2meZ2e4 ,如果用 q 表示原子核带电,则有 E=−8ϵ02h2n2meq2e2
- 做题
- ΔE 越大, ν 越大, λ 越小。
- 巴耳末系有四条谱线是可见光
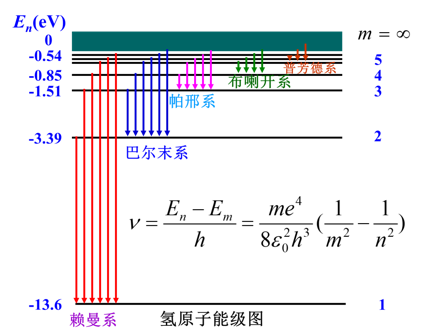 ,分别是3/4/5/6到2
,分别是3/4/5/6到2
- 第一激发态对应能级为2的谱线
- 氢原子光谱中:
- 波长最短的光子能量: hν=13.6(1−m21)
- 波长最长的光子能量: hν=13.6[m21−(m+1)21]
- 单色光照射处于基态的氢原子,由于氢原子吸收了一部分光能(电子跃迁),故而透射光会比入射光弱。
物质波
E=hν
λ=ph
- 值得注意的是,在这里,由于物质粒子与光子不同,并不以光速运动,故而:ν=λc 的公式不再适用,当我们计算粒子(非光子)的德布罗意波长时,建议直接使用 λ=ph 这个式子进行计算。
- 不考虑相对论效应时,有
E=2mp2
- 当考虑相对论效应时,由相对论公式 E2=E02+c2p2 ,可得:
λ=Ek2+2Ekm0c2hc
若 Ek≪m0c2 ,则有:
λ≈2Ekm0c2hc=2m0Ekh
若 Ek≫m0c2 ,则有:
λ=Ek 2hc=Ekhc
- 能量量子化可以视为某种“驻波”的表现:
- 设这个驻波两端相距 L 且固定,有 sinkL=0 ,就有 kL=nπ ,其中 k=λ2π ,则可以得到 λ=n2L 。
- 如果氢原子周围形成环形驻波,则有 2πr=nλ ,与 λ=ph 联立,可以求得 L=2πnh ,就是玻尔的轨道量子化条件。
- 实验验证(戴维逊-革末实验):
- X射线衍射
- 出现干涉时,电流表示数极大,同时假设电子加速电压 U ,有 21mv2=eU ,其中 v=m2eU ,而 λ=mvh=2emUh ,可以与上面的式子联立求解。
- 由于 m 可以是任何整数,固定 θ 角,改变加速电压,会出现多次电流极大。
- 实验验证(汤姆孙实验/约恩逊实验)
- 应用
- 电子显微镜分辨率远大于光学显微镜分辨率
- 由圆孔衍射的公式可以知道光学仪器的线分辨极限 δy=Δθmf=d1.22λf ,分辨本领为 δy1=1.22λ1fd 。
- 做题
- 如果例子在 x 方向动量为 px , y 方向动量为 py , z 方向为 pz ,那么粒子的能量 E=2px2+py2+pz2
量子力学
波函数与其统计解释
- 物质波可以用随时间和空间变化的函数来表示,称为波函数。
- 一维空间 Ψ(x,t) ,三维空间 Ψ(r,t) ,对应的德布罗意波的频率 ν=hE ,波长 λ=ph
- 自由粒子的物质波是单色平面波
- Ψ(x,t)=Ψ0cos2π(νt−λx)=Ψ0cosh2π(Et−px)
- 写成复数形式 Ψ(x,t)=Ψ0eipx/ℏe−iEt/ℏ
- 波函数的物理意义
- 错误看法:波由粒子组成/粒子由波组成
- 光强决定光子在空间各处出现的概率
- 光是概率波(一次入射一个光子,经过足够长时间,衍射图像与一次入射很多光子所得衍射图像相同)
- 波��函数的统计解释
- 波函数模的平方 ∣Ψ(r,t)∣2 代表 t 时刻,在 r 处粒子出现的概率密度
- 粒子在体积元 dV 内出现的概率为 ∣Ψ∣2dV=ΨΨ∗dV
- 波函数满足的条件
- 标准条件:单值、有限、连续
- 如果只给出了在某一段中的波函数,那么它在这段儿的两端的波函数值都为 0
- 归一化条件: ∫V∣Ψ∣dV≡1
- 波函数 Ψ 与波函数 Ψ′=cΨ 描写的是粒子的同一状态,因为粒子在空间格点的概率只决定于波函数在空间个点的相对强度而非绝对大小。
- 对单个粒子 ∣Ψ∣2 给出粒子的概率分布密度
- 对多个粒子 N∣Ψ∣2 给出粒子数的分布密度
不确定关系
σAσB≥21∣⟨[A,B]⟩∣
左侧是两个物理量的标准差(不确定性),右侧是两个物理量对易子的期望值的一半(注意要加绝对值)
- 位置-动量
- Δx⋅Δpx≥2ℏ , y , z 方向同理。
- 当激光的谱线宽度为 Δλ 时, Δpx 的值为: Δpx=λ2hΔλ (利用积分)
- 能量-时间
- ΔE⋅Δt≥2ℏ
- Δt - 粒子处在某量子态的寿命
- ΔE - 该量子态能量的不确定范围
- 做题:
- 单缝夫琅禾费衍射(见大物笔记)
- 双缝干涉(见大物笔记)
- 计算相干长度:由于激光的谱线不为 0 ,激光的波列长度不是无限长。光子沿 x 轴方向传播时, x 坐标的不确定度就是相干长度。
- 经典力学中,质量为 m ,圆频率为 w 的线性谐振子的动量为 p 时,振子的能量是 E=2mp2+21mw2x2 ,由于势能的对称性,粒子坐标与动量平均值为 0 ,所以 Δx2=x2
- 原子谱线自然宽度,实际上就是 Δν ,标志谱线单色性好坏的物理量。
薛定谔方程
iℏ∂t∂Ψ(x,t)=−2mℏ2∂x2∂2Ψ(x,t)
iℏ∂t∂Ψ(x,t)=[−2mℏ2∂x2∂2+U(x,t)]Ψ(x,t)
其中令能量算符/哈密顿算符为
H^=−2mℏ2∂x2∂2+U(x,t)
于是含时薛定谔方程:
iℏ∂t∂Ψ(x,t)=H^Ψ(x,t)
E=2mpx2+py2+pz2+U(r,t)
对应的哈密顿算符:
H^=−2mℏ2(∂x2∂2+∂y2∂2+∂z2∂2)+U(r,t)=−2mℏ2∇2+U(r,t)
其中
∇=∂x∂i+∂y∂j+∂z∂k
H^=i∑ [−2mℏ2(∂xi2∂2+∂yi2∂2+∂zi2∂2)]+U(r1,r2,⋯,t)
- 薛定谔方程是关于时间的一阶偏微分方程,知道初始时刻波函数就可以确定以后任何时刻的波函数
- 薛定谔方程的解满足叠加原理
定态薛定谔方程
- 势场稳定, U 与时间无关,称为定态问题,表示粒子出现在空间的概率与时间无关,可以用分离变量法求解。
- 分解为以下两个方程
iℏ dtdT(t)=ET(t)
H^Φ(r)=EΦ(r)
- 可以解出: T(t)∝e−ℏiEt ,第二个�方程的解则为 Φ(r) 。即:
Ψ(r,t)=Φ(r)e−ℏiEt
ρ(r,t)=Ψ(r,t)2=Φ(r)e−ℏiEt2=Φ(r)2
(消去了含时的虚数部分)
- 求解定态问题的步骤:
- 列出定态薛定谔方程
- 根据波函数的连续,单值,有界性求解能量 E
- 写出对应能量本征值的波函数
- 通过归一化确定归一化系数
- 一般波函数可以使用态叠加原理得到
Ψ(r,t)=n∑CnΨn(r,t)=n∑CnΦn(r)e−iEnt/ℏ
薛定谔方程的矩阵形式
动量表象
ψp(x)=2πℏ1eipx/ℏ
它组成一个完备系,状态 Ψ 可以按照其展开
Ψ(x,t)=∫C(p,t)ψp(x)dp
其中 C(p,t) 可以用以下方式求出
C(p,t)=∫ψp∗(x)Ψ(x,t)dx
- Ψ(x,t) 和 C(p,t) 一一对应, Ψ(x,t) 是该状态在坐标表象中的波函数; C(p,t) 是该状态在动量表象中的坐标函数。
含时薛定谔方程的矩阵形式
Ψ(x,t)=n∑Cn(t)ϕn(x)
可以求出:
iℏdtdCm(t)=n∑ HmnCn(t)
其中:
Hmn=⟨ψm∣H^∣ψn⟩
写成矩阵形式
iℏdtdC1(t)dtdtdC1(t)dtdCn(t)dtdCn(t)=H11H21⋯Hn1⋯H12H22⋯Hn2⋯⋯⋯⋯⋯⋯H1nH2n⋯Hnn⋯⋯⋯⋯⋯⋯C1(t)C2(t)⋮Cn(t)⋮
- 由于力学量算符都是厄密算符,根据厄密算符的性质可以推出
Hmn=Hnm∗
∫−∞+∞Φm∗Φndx=δmn
定态薛定谔方程的矩阵形式
Ψ(x)=n∑Cnψn(x)
可以推出:
n∑Cn⟨ψm∣H^∣ψn⟩=En∑Cn⟨ψm∣∣ψn⟩
其中:
⟨ψm∣∣ψn⟩=δmn
Hmn=⟨ψm∣H^∣ψn⟩
得出:
n∑ (Hmn−Eδmn)Cn=0
Fmn=Fnm∗
Fmm=Fmm∗
H11−EH21⋯Hn1⋯H12H22−E⋯Hn2⋯⋯⋯⋯⋯⋯H1nH2n⋯Hnn−E⋯⋯⋯⋯⋯C1C2⋮Cn⋮⋮=0
- 这个线性齐次方程组(称为久期方程)有非零解的条件是系数行列式等于 0
H11−EH21⋯Hn1⋯H12H22−E⋯Hn2⋯⋯⋯⋯⋯⋯H1nH2n⋯Hnn−E⋯⋯⋯⋯⋯=0
解这个方程,可以得到一组 E 值,把求得的 E 值分别代回方程组,可以求得对应的本征矢。注意求出后要归一化 ∣c1∣2+∣c2∣2+⋯=1 。
本征矢为:
ψi=C1C2⋮Cn⋮
- 对于含时的波函数,将初始时的波函数做能量本征矢的线性展开
Ψ=A1⋮An⋮=a1ψ1+a2ψ2+…
对波函数进行测量时,测量值的结果是能量本征值之一 Ei ,概率为 ∣ai∣2 。测量能量的统计平均值为 E=∑Ei∣ai∣2
- 求得 ai 后,乘以能量本征波函数的时间部分,得任意时刻的波函数
ψ(t)=a1e−iℏE1tψ1+a2e−iℏE2tψ2+⋯
- 计算能量平均值时,也可以使用 ⟨ψ∣H∣ψ⟩ 计算系统的能量值(不是动能),具体操作就是直接做矩阵乘法。
- 在谐振动中 U=21kx2=21mw2x2
- 力学量用算符表示——处于某一状态时,力学量不具有确定值,只能通过一系列可能值计算其平均值。算符可以帮助计算这些平均值。
- 作用在一个函数上得到另一个函数
算符的运算规则
- [A^,B^+C^]=[A^,B^]+[A^,C^]
- [A^,B^C^]=[A^,B^]C^+B^[A^,C^]
- [B^C^,A^]=[B^,A^]C^+B^[C^,A^]
- [A^,[B^,C^]]+[B^,[C^,A^]]+[C^,[A^,B^]]=0
本征值和本征态
- 算符 F^ 对应的本征值 λ ,本征函数 ψ ,则该算符满足本征值方程
F^ψ=λψ
- 定态薛定谔方程实质上是求哈密顿算符的本征值的问题,其中 Ψ(r) 是本征函数,E 为本征值。
H^Φ(r)=EΦ(r)
- 另一个假设是波函数随时间的演化满足薛定谔方程。
- 量子力学理论中的对应:系统处于量子态 Ψ 时,对力学量 F^ 进行测量(这里由于 F^ 是有意义的力学量的算符,故而 F^ 一定是厄密算符)
- 力学量 ↔ 算符
- 力学量的可能取值 ↔ 算符的本征值
- 测量结果为 F^n 的概率为 ∣cn∣2=∣∫ψn∗Ψdx∣2
- 同时 F=∑nFn∣cn∣2 其中 Fn 是 ψn 本征函数对应的本征值。(对于连续的量比如 <p^x> 其平均值就为 ∫−∞∞px∣cpx∣2dpxdx (类似于信号与系统里面的类比)
- ∑n∣Cn∣2=1
- 某个量的概率分布函数 ∣cn∣2
- 某个态出现的概率与时间无关
厄密算符
- 厄密算符 F^=F^(x,y,z) 定义:
∫ψ∗F^φdxdydz=∫φ(F^ψ)∗dxdydz
式中 ψ 和 ϕ 分别为在无穷远处趋于 0 的任意函数。
- 性质
- 对系统的任意量子态,厄密算符的平均值必为实数。 F=∫ψ∗F^ψdx=∫ψ(F^ψ)∗dx=(∫ψ∗F^ψdx)∗=F∗
- 厄密算符的本征值为实数
- 由于力学量算符的本征值就是力学量的可能取值,故而量子力学中的任何力学量一定是厄密算符。
- 厄密算符必须是可观测量
- 厄密算符属于不同本征值的本征函数彼此正交,为正交归一的完全集,物理上合理的波函数都可以用这个正交归一的完全集展开。
- 也即 Ψ=∑ncnψn , Ψ(r,t)=∑ncnΨn(r,t)=∑ncnΦn(re−iEnt/ℏ) (注意含时项中的 En 是与对应的 p 一致的
- 且 cm=∫ψm∗Ψdx
- 题目中求 cn 的办法:
- 直接代入进行凑配
- 使用公式(用xxx展开, ψm∗ 就是那个xxx)
算符对易与共同本征函数
- 对易:如果俩算符满足 F^G^=G^F^ ,那么这两个算符对易。
- 如果两个力学量算符有一组共同完备的本征函数系,那么两算符对易。
- 一组力学量算符具有共同完备本征值函数系的充要条件是这组算符两两对易。(不考虑简并态)
- 力学量完全集合:为完全确定状态所需要的一组两两对易的力学量算符的最小数目集合称为力学量完全集。
- 力学量完全集中,力学量的数目一般与体系自由度数相同
- 力学量完全集确定的本征函数系构成态空间的一组完备的本征函数,体系的任何状态均可用它展开。
- 例子:三维空间中自由粒子,完全确定其状态需要 p^x p^y p^z 这三个两两对易的力学量
- 寻找力学量完成集:首先看自由度个数,其次找不对易的值
- 计算:
- [F^,G^] 作用在波函数 ψ 上
- 利用之前计算出的其他算符的对易关系进行计算(注意在这里交换律不一定成立,要考虑其他算符的对易性)
- 需要记忆的一些对易
- [x,p^x]=iℏ , [y,p^x]=0
- 角动量算符
- 角动量平方算符
算符们
能量算符 E^
- E^=iℏ∂t∂
动量算符 p^
- p=p^=−iℏ∇
- p^x=−iℏ∂x∂
- 动量算符是厄密算符(通过分步积分)
- 本征方程:
- iℏ∇Φpˉ(r)=pΦpˉ(r)
- 解得: Φp(r)=(2πℏ)3/21exp(ℏip⋅r)
- 动能算符 T^=2mpx2^=−2mℏ2∂x2∂2 ,也是厄密算符
- 本征方程: T^Φp(r)=2mℏ2∇2Φp(r)=2mp2Φp(r)
- 动量的本征函数 = 动能的本征函数
- 与动量不同的是,动量的本征值是 p ,而动能的本征值是 2mp2
- 自由例子的动量和能量可以同时取确定值
- 动量算符相互对易
- 动量算符与动能算符相互对易
哈密顿算符 H^
- H^=2mp^2+U(r)=−2mℏ2∇2+U(r)
角动量算符 L^
L^x=yp^z−zp^y=−iℏ(y∂z∂−z∂y∂)L^y=zp^x−xp^z=−iℏ(z∂x∂−x∂z∂)L^z=xp^y−yp^x=−iℏ(x∂y∂−y∂x∂)
- 角动量算符的对易关系: ^9dc03c
- [L^x,L^y]=iℏL^z
- [L^y,L^z]=iℏL^x
- [L^z,L^x]=iℏL^y (注意这里 L^z 和 L^x 的次序)
- 证明角动量算符对易相关:如果前面的系数与对易的两项都无关,就可以提出来
- [yp^z,xp^z] 可以提出 yx[p^z,p^z]
角动量平方算�符
L2^=L^⋅L^=Lx2^+L^y2+L^z2
[L^2,L^x]=[L^2,L^y]=[L^2,L^z]=0
L2^=−ℏ2[sinθ1∂θ∂(sinθ∂θ∂)+sin2θ1∂φ2∂2]
L^2Y=−ℏ2[sinθ1∂θ∂(sinθ∂θ∂)+sin2θ1∂φ2∂2]Y=μℏ2Y
通过求解上述方程,可以得到:
L^2Ylml=l(l+1)ℏ2Ylml
L^zYlml(θ,ϕ)=mlℏYlml(θ,ϕ)
其中: l=0,1,2,… , ml=l,l−1,l−2,…,−l+1,−l 。
态叠加原理
- Ψ1(x,t) 是粒子运动的一个态, Ψ2(x,t) 是描述粒子运动的一个态,则它们的线性叠加也是描述粒子运动的一个态
Ψ(x,t)=c1Ψ1(x,t)+c2Ψ2(x,t)
Ψ=i∑Ciφi
ϕ1 为算符 F^ 的本征态,对应的本征值为 λi ,对力学量 F 进行测量,测量结果可能是本征值中的任何一个,出现 λi 的概率为 ∣Ci∣2 。
量子力学的其他假设/知识
交换与粒子的分类
- 对两个同类粒子进行交换,不会改变系统的状态,因为在量子力学中没有确定的轨道方程,对于内禀属性完全相同的粒子是不可分辨的。
- 对任意两个同类粒子进行交换,波函数的模不变,也即 Ψ(1,…,i,…,j,…,N)=eiθΨ(1,…,j,…,i,…,N) ,其中 θ 为实数
- 粒子的分类
- 玻色子: θ=0 , Ψ(1,⋯,i,⋯,j,⋯,N)=Ψ(1,⋯,j,⋯,i,⋯,N) 。自旋量子数取整数,全同玻色系统波函数对于任意一对粒子交换而言是不变的
- 费米子: θ=π , Ψ(1,⋯,i,⋯,j,⋯,N)=−Ψ(1,⋯,j,⋯,i,⋯,N) 。自旋量子数取半整数,如 21,23 等,全同费米系统的波函数对于任意一对粒子交换而言改变符号,是反对称的。
不确定关系
- 当两个算符不对易且满足 [F^,G^]=ik^ 时,有 \overline{ {\left( \Delta\hat{F} \right)^{2} }} \cdot\overline{ {\left( \Delta\hat{G} \right)^{2} }} \geq\frac{\overline{ {k} } \,^{2} } {4}
- 其中 (ΔF^)2=F^2−F2 (譬如 (Δx)2=x2−x2 )
概率守恒
- 概率守恒:单位时间内在有限体积内发现例子的概率的增量等于通过体积表面流入的概率。
- 概率守恒方程的微分形式
∂t∂(∣Ψ∣2)=−∇⋅j
其中 j 为概率流密度矢量
j=2miℏ(Ψ∇Ψ∗−Ψ∗∇Ψ)
狄拉克符号
- 用右矢 ∣ψ⟩ 表示一个量子系统的状态,左矢 ⟨ψ∣ 表示右矢的复共轭转置。二者一起构成了希尔伯特空间的对偶性。
- 左矢和右矢可以进行��内积运算,表示为 ⟨ψ∣∣ϕ⟩,这会得到一个复数或实数,表示两个量子态之间的重叠程度。如果两个量子态完全相同,则内积为 1 。在实际计算中 ∫ψm∗(x)ψn(x)dx=⟨ψm∣∣ψn⟩
- 算��符一般作用于右矢,例如 A^∣ψ⟩
- 计算概率(期望值),算符 A^ 对于量子态 ∣ψ⟩ 的期望值为 ⟨ψ∣A^∣ψ⟩ 。
宇称问题
- 在一维势场中运动的粒子,势能对原点对称 U(−x)=U(x) , Φ(−x)=±Φ(x)
- 宇称是函数在空间反演下表现出的特性,类似于奇偶函数 or 一个矢量被镜面翻转之后具有怎样的特性。
- P 空间反演算符
- 偶宇称: Pψ(x)=ψ(−x)=ψ(x)
- 奇宇称: Pψ(x)=ψ(−x)=−ψ(x)
量子力学应用
一维定态问题
开局一张图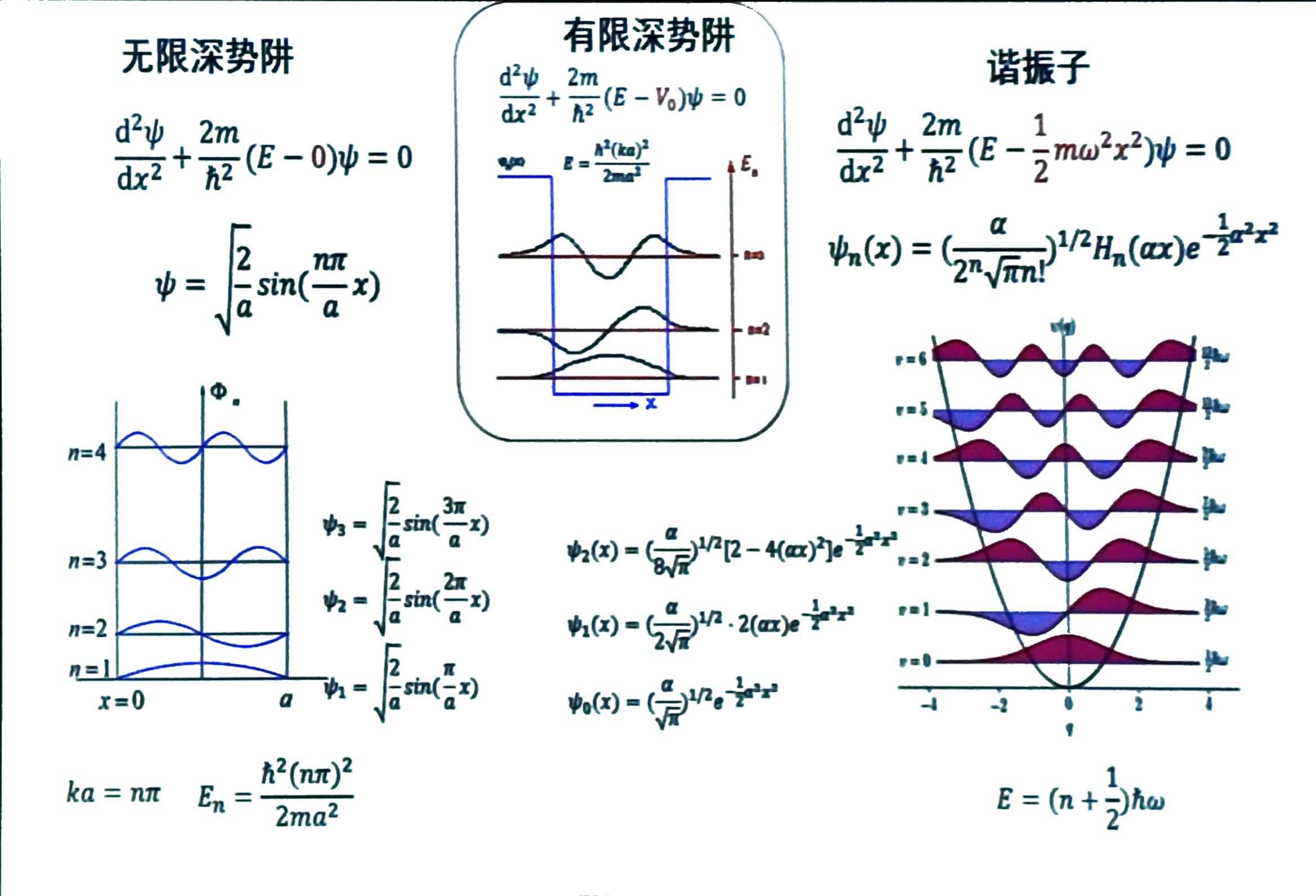
无限深势阱
H={−2mdx2ℏ2d2,−2mdx2ℏ2d2+∞,0⩽x⩽Lx<0,x>L
Φn(x)={L2sinLnπx,0,0⩽x⩽L0>x,x>L
- 在势阱中粒子波函数是驻波, Φn(x) 有 n 个最大值和最小值, ∣Φn(x)∣2 有 n 个最大值。参考图:
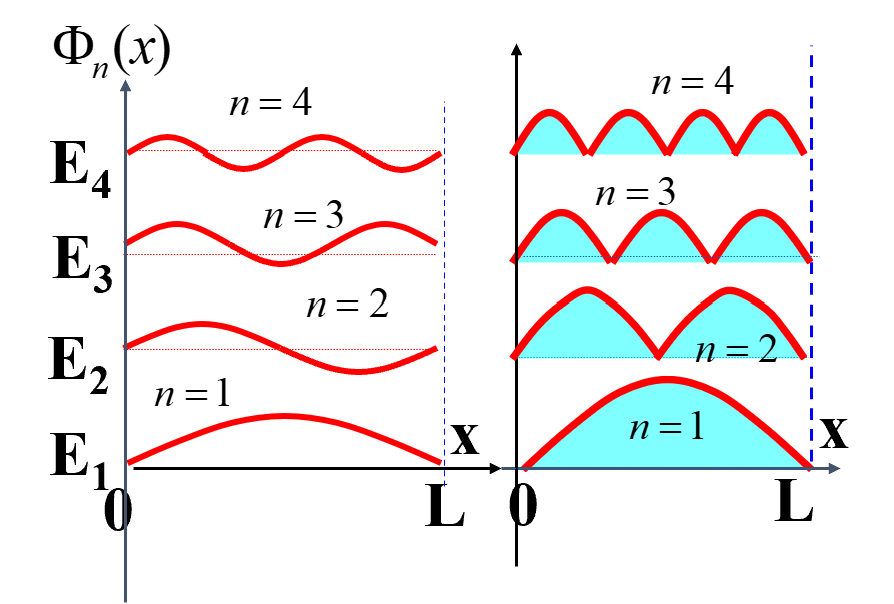
- 能量本征值
En=n2E1=n22mL2π2ℏ2
ΔEn=En+1−En=(2n+1)E1=(2n+1)2mL2π2ℏ2
- 微观粒子的质量越小,粒子的能级间隔越大,量子效应越明显,质量变大时 ΔE→0 ,量子效应消失
- 势阱宽度越小,能级间隔越大,量子效应明显。势阱宽度 L→∞ 时 ΔE→0
- n→∞ 时, EnΔEn=n22n+1→0 ,能量连续
- 势阱中粒子的动量:
pn=±2mEn=±nLπℏ=±2Lnh
λn=∣pn∣h=n2L
- 发现势阱宽度恰好是粒子半波长的整数倍 L=2Nλn ,势阱中粒子的每一个能态( n 确定)对应的波函数为一个特定波长的驻波。
- 可以将波函数转化成 e 指数形式( sinx=2i1(eix−e−ix) ),于是
Ψn(x,t)=Φn(x)e−ℏiEnt=21L2[e−ℏi(Ent−pnx)−e−ℏi(Ent+pnx)]=C1e−ℏi(Ent−pnx)+C2e−ℏi(Ent+pnx)
- 一维无限深势阱中粒子波函数是正交归一的
- ∫−∞+∞Φm∗Φndx=δmn ( m=n 时, δmn=1 ,其它时候 δmn=0 。
- n 不能取 0 ,因为这代表着没有粒子,也不能取负整数,因为相当于对定态波函数乘 −1 ,但这两个波函数描述的粒子概率分布相同,能量也相同,所以无论 n 取正/负,二者描述的状态并无区别。
- 三维无限深势阱:
- 分解为三个独立的一维无限深势阱的定态薛定谔方程
- Φ(x,y,z)=X(x)Y(y)Z(z)
- 2mℏ2(∂x2∂2+∂y2∂2+∂z2∂2)Φ(x,y,z)=EΦ(x,y,z)→
- −2mℏ2dx2d2X=E1X
- −2mℏ2dy2d2Y=E2Y
- −2mℏ2dz2d2Z=E3Z
- E=E1+E2+E3
势阱与隧穿
- 在量子力学中不管粒子的初始动能多大,遇到有限势垒后反射和透射总是同时存在。
- 设 V(x) 在 x=a 处有一个有限的跳跃,则能量本征波函数 ψ(x) 及其导数 ψ′(x) 在 a 点必定连续
- 束缚态与散射态
- 束缚态时,粒子在有限空间内运动: x→±∞ , Φ(x)→0 , E<U(x) ,能量分立(相比散射态多一个边界条件)
- 散射态时,粒子运动到无穷远处: x→±∞ , Φ(x)↛0 ,能量连续
- 一般表示形式:行波解,以 e 指数形式呈现
- 对于平面波 Ψ(r,t)=Aei(k⋅r−wt) 的概率流密度为: j=∣A∣2mℏk (注意反射波的概率流密度是负数)
- 透射系数 T=jjT
- 反射系数 R=j∣jR∣
- T+R=1
- 这一部分要用到的数学,参见
- 微分方程的解法(见半导体物理知识总结高数知识Recall)
- 行波解(见半导体物理知识总结)
- 驻波解 (见半导体物理知识总结)
一维谐振子
- 晶体原子位于其他原子的势场中,原子围绕平衡位置做小振动,可近似认为做简谐振动,势能函数
U(x)=21kx2
H^=−2mℏ2dx2d2+21kx2
(−2mdx2ℏ2d2+21kx2)Φ(x)=EΦ(x)
dx2d2Φ+ℏ22m(E−21mω2x2)Φ=0
(后面式中 w=mk 是谐振子角频率,求谐振子最重要的就是求 w)
En=(n+21)ℏω
En+1−En=ℏω=hν
- 当 n=0 时能量最小,零点能为 E0=21ℏw
- 谐振子的定态波函数
Φn(x)=(2nπn!α)1/2Hn(αx)e−21a2x2
其中 α=ℏmw , Hn 为厄米特多项式。
Φ0(x)=(πα)1/2e−21α2x2
Φ1(x)=(2πα)1/2⋅2(αx)e−21a2x2
Φ2(x)=(8πα)1/2[2−4(αx)2]e−21α2x2
- 其中,谐振子波函数满足正交归一: ∫∞+∞Φm(x)Φn(x)dx=δmn
- 与经典振子不同,量子振子可以穿入势阱壁内部,具有隧穿效应。
- 当 n→∞ 时,量子概率分布趋于经典概率分布
- 谐振子势能的平均值可以用 U=21mw2x2
- 求基态微观线性谐振子的“经典界限”:通过 21mw2A2=21ℏw (右侧能量可以根据题目条件发生变动。
- 当谐振子的波函数为例如 H^=−2mℏ2dz2d2+mgz+21mw2z2 时,配凑为为 21mw′2 的形式(配凑的方法是:化成 21mw2x2−2mℏdx2d2 的形式),把剩下的常数项放在后面即可,如此例中的 En′=En−2w2mg2 ,而 z′=z+w2g
- 一个配凑的例子:对于 H^=2m1(p^x2+p^y2)+21mw2(x2+y2)+λxy ,配凑为: x′=21(x+y) , y′=21(x−y) ,使得 H^=−2mℏ2(∂x′2∂2+∂y′2∂2)+21mω2(x′2+y′2)+2λ(x′2−y′2)=H^x′+H^y′ ,其中: H^x′=2mP^x′2+21mωx′2x′2 ωx′2=ω2+mλ H^y′=2mP^y′2+21mωy′2y′2 ωy′2=ω2−mλy2 ,最后得到:(H^x′+H^y′)Φn(ℏmωy′x′)Φl(ℏmωy′y′)=[(n+21)hωx′+(l+21)hωy′]Φn(ℏmωx′x′)Φl(ℏmωy′y′)
- 对于二维谐振子:由于其波函数为 Φ(x,y)=ϕ(x)ϕ(y) ,其本征值为各方向分量相加(某个方向的本征方程两端先乘剩下两个波函数,之后相加)
氢原子
U(r)=−4πϵore2
[−2mℏ2∇2−4πε0re2]Φ=EΦ
其中:
∇2=r21∂r∂(r2∂r∂)+r2sinθ1∂θ∂(sinθ∂θ∂)+r2sin2θ1∂φ2∂2
由于:
L2^=L^⋅L^=L^x2+L^y2+L^z2=−ℏ2[sinθ1∂θ∂(sinθ∂θ∂)+sin2θ1∂φ2∂2]
故而可以有:
[−2mr2ℏ2∂r∂(r2∂r∂)+2mr2L2^−4πε0re2]Φ=EΦ
由于: H^ , L2^ 和 L^z 两两对易,所以要确定一个氢原子的状态需要上述三个力学量。
由于上面已经求出了角动量平方算符和角动量算符的本征方程:
L2^Ylml=l(l+1)ℏ2YlmlL^zYlml(θ,φ)=mlℏYlml(θ,φ)
可以利用上述方程的性质得到特征函数:
[−2mr2ℏ2∂r∂(r2∂r∂)+2mr2L^2−4πε0re2]R(r)Ylml(θ,φ)=ER(r)Ylml(θ,φ)
并将 L^2 用其特征值代替,得到
[−2nr2ℏ2∂r∂(r2∂r∂)+2nr2ℏ2l(l+1)−4πϵ0re2]R(r)=ER(r)
最终解出:
Φnlml(r,θ,φ)=Rnl(r)Ylml(θ,φ)
En=−2ℏ2(4πε0)2me4n21
其中 n=1,2,… 为主量子数, l=0,1,2,…,n−1 为轨道量子数, ml=l,l−1,l−2,…,−l+1,−l 为磁量子数。
- 概率相关
- 测量值为 En 的概率为 ∑lml∣Cnlml∣2 (氢原子的能量只与主量子数 n 有关)
- 角动量平方测量值为 l(l+1)ℏ2 的概率为 ∑ml∣Cnlml∣2
- 角动量分量 Lz 的测量值为 mlℏ 的概率为 ∣Cnlml∣2
- 在空间点 (r,θ,ϕ) 处, dV 中电子出现的概率为 ∣Φnlml(r,θ,ϕ)∣2dV=[∣Rnl(r)∣2dr]⋅[∣Ylml(θ,ϕ)∣2sinθdrdθdϕ] ,其中 dΩ=sinθdθdϕ
- 电子径向概率分布 Wnl(r)dr=[∫∣Ylm(θ,ϕ)∣2dΩ]Rnl2(r)r2dr
- 把整个函数转换为只依赖于 r 的函数 P(r)=∫02π∫0πρ(r,θ,ϕ)sinθdθdϕ
- 电子沿径向的概率分布是连续的,在某处概率最大,与经典轨道对应。(注意这里不用做积分)
- 电子角向概率分布 Wnl(θ,ϕ)dΩ=[∫Rnl2(r)r2dr]∣Ylm(θ,ϕ)∣2dΩ (注意这里不用做积分)
塞曼效应
- 在外磁场中,氢原子从激发态跃迁到基态时,发射光谱不止一条谱线。
- 电子轨道角动量导致轨道磁矩 μl=−2meL ,因此具有附加磁能 ΔE=−μl⋅B=2meLzB ,于是
H^=−2mr2ℏ2∂r∂(r2∂r∂)+2mr2L^2−4πε0re2+2meL^zB
[−2mr2ℏ2∂r∂(r2∂r∂)+2mr2ℏ2l(l+1)−4πε0re2+2meBmlℏ]Rnl(r)=EnlnlRnl(r)
- 解得 Enlml 为
Enlml=En+2meBmlℏ =−8ϵ02h2n2mee4+mlμBB
其中 μB=2meℏ ,为玻尔磁子。由于 ml 可以取不同值,故而能级会出现分裂。
电子的自旋
- 通过斯特恩-盖拉赫实验(出现反常塞曼效应)可以得知银原子虽然没有轨道磁矩,但有其它磁矩,认为银原子中未配对的价电子具有自旋角动量与自旋磁矩。
- 定义自旋角动量 S (有轨道角动量的量纲),有 x,y,z 三个分量
- 对易关系
- [S^i,S^j]=iℏεijkS^k
- [S^2,S^i]=0
- S^2 的本征值为 s(s+1)ℏ2 ,其中 s 是自旋量子数,可取不小于 0 的整数和半整数
- S^z 的本征值是 msℏ ,其中 ms 是自旋磁量子数,可取整数或者半整数, ms=s,s−1,…,−s+1,−s 共 2s+1 种取值。
- S^2 与 S^z 的共同的本征态 χms 用 s 和 ms 来表征。
- 电子自旋量子数 s=21 ,电子自旋磁量子数 ms=±21
- 电子的共同本征态:
- χ1/2=∣1/2,1/2⟩≐∣↑⟩=∣1⟩
- χ−1/2=∣1/2,−1/2⟩≐∣↓⟩=∣2⟩
- 更数学地,用 ∣↑⟩=(10) , ∣↓⟩=(01) 表示上述两个本征态(也可以从矩阵表示那里反推)
- 两个本征态有如下性质
- 正交:⟨↑∣↓⟩=0
- 归一:⟨↑∣↑⟩=⟨↓∣↓⟩=1
- 完备:∣↑⟩⟨↑∣+∣↓⟩⟨↓∣=I
- 任何基矢可以看作:
∣ψ⟩=c1∣↑⟩+c2∣↓⟩=(c2c1)
- S2 在 (S2,Sz) 表象的矩阵表示:
S2=(⟨1∣S2∣1⟩⟨2∣S2∣1⟩⟨1∣S2∣2⟩⟨2∣S2∣2⟩)=43ℏ(1001)
- Sz 在 (S2,Sz) 表象的矩阵表示:Sz=21ℏ(100−1)
- 为简化计算,引入无量纲的泡利自旋算符 σ^ :
S^=2ℏσ^
[S^i,S^j]=iℏεijkS^k⇒4ℏ2[σi^,σj^]=iℏεijk2ℏσk^⇒[σi^,σj^]=2iεijkσk^
- 泡利矩阵是泡利算符在 (S2,Sz) 表象的矩阵表示:
σx=(0110)σy=(0i−i0)σz=(100−1)
σ^2=σ^x2+σ^y2+σ^z2=3(1001)=3Iσ^x2=σ^y2=σ^z2=I=(1001)
σ^xσ^y=−σ^yσ^x=iσ^z
- 约定俗成:波函数中,一般第一个自旋为 21 ,第二个自旋为 −21
泡利不相容原理
- 四个量子数
- 主量子数 n=1,2,3,…
- 轨道角量子数:l=0,1,2,3,…,(n−1)
- 轨道磁量子数: ml=0,±1,±2,…,±l
- 自旋量子数: ms=±21
- 每一壳层( n 相同)能容纳的电子数: 2n2
- 每一支壳层( l 相同时)能容纳的电子数: 2(2l+1)
- 填充顺序 1s→2s→2p→3s→3p→4s→3d→4p→5s→4d→5p→6s→4f→5d→6p→7s→5f→6d
双态过程
- 有两个能级的量子系统,互相靠得很近,距离其他能级又比较远,与其他能级之间的跃迁无需考虑。
薛定谔方程的矩阵形式
- 利用狄拉克矢量表示:波函数 ψ(t) ,可以表示为 ∣ψ(t)⟩ ,称为态矢量,一套完备正交归一函数 ψj 表示为 ∣j⟩ ,称为基矢,则 ∣ψ(t)⟩=∑jCj∣j⟩ , Cj=⟨j∣∣ψ(t)⟩ ,意为态矢量 ∣ψ(t)⟩ 处于 ∣j⟩ 的概率幅
- 代入薛定谔方程可以求得:
iℏ∂t∂⟨iψ(t)⟩=j∑⟨iH^j⟩⟨jψ(t)⟩
也即:
iℏ∂t∂Ci=j∑HijCj
其中 Hij=∫ϕi∗H^ϕjdx ,由厄密算符的性质可知 Hij∗=Hji
iℏ∂t∂(C1C2)=(H11H21H12H22)(C1C2)
上面的矩阵是有关哈密顿量与时间的,下面去求各个哈密顿量及其本征值,从而得到其能量值。我们知道 Hαβ=⟨α∣H^∣β⟩=Eαδαβ ,则哈密顿矩阵
(H11H21H12H22)=(E100E2)
iℏ∂t∂(C1C2)=(E100E2)(C1C2)
于是得到 iℏ∂t∂Ci=EiCi ,解这个微分方程,得到 Cα(t)=Cα(0)e−iEαt/ℏ ,由于时间项是虚数,故而 ∣Cα∣2 与时间无关。
氨分子的双态过程
- 氨分子中 N 原子有一对镜像对称位置,对应的量子态分别为 ∣1⟩=(10) 和 ∣2⟩=(01) 。要研究这个系统状态的实际情况。
- 在实际情�况中,氨分子可以在 ∣1⟩ 和 ∣2⟩ 这两个状况下来回变化,在其表象中,其哈密顿算符的矩阵表示为
H=(E0AAE0)
其中 H12=H21=A<0 。对角化上式矩阵,能量本征值 E±=E0±A ,能级分裂,间隔为 ∣2A∣ ,对应的本征态为 ∣χ±⟩=21(∣1⟩±∣2⟩) 。因此,我们可以把方程
iℏ∂t∂(C2C1)=(E0AAE0)(C2C1) 转化为 iℏ∂t∂(C+C−)=(E0+A00E0−A)(C+C−) ,从而求出:
C±(t)=C±(0)e−iℏE±t
用本征态表示 c1 与 c2 ,则有
C1(t)=21(C+(t)+C−(t))=21(C+(0)e−iℏE+t+C−(0)e−iℏE−t)
C2(t)=21(C+(t)−C−(t))=21(C+(0)e−iℏE+t−C−(0)e−iℏE−t)
若 C+(0)=C−(0)=21 ,则
C1(t)=e−iℏE0tcosℏAtC2(t)=−ie−iℏE0tsinℏAt
系统分别处于 ∣1⟩ 和 ∣2⟩ 态的几率为
P1=∣C1(t)∣2=cos2ℏAt
P2=∣C2(t)∣2=sin2ℏAt
- 概率密度要平方之后计算
- 不确定度计算是 Δx 而不是 x
- 态叠加原理的计算中也要注意各个波函数的条件(单值/有限/连续)
- 取模后平方是共轭啊喂!!!
- 能量 E=T+V
- 求 ψ(t) 的时候别忘了乘能量项
- 计算衍射图样最大宽度,注意上下都要乘2
- 不确定关系那里是 2ℏ ,注意 ℏ 和 h 的不同
- 波函数概率密度最大位置可以有多��个
奇奇怪怪


 ,分别是3/4/5/6到2
,分别是3/4/5/6到2
