固体物理
参考:
固体类型
- 无定形:在原子/分子的尺度内有序
- 单晶:晶粒,由晶界彼此分离,几何周期性好
- 多晶:在多个原子/分子的尺度上有序,称为单晶区域,有不同的大小方向。
空间晶格
- 晶格:晶体中原子的周期性排列
- 晶胞/单胞:可以复制出整个晶体的一小部分晶体
- 初基原胞:最小晶胞
- 三维晶体中的每一个等效格点都可用矢量 r=pa+qb+sc 表示, p , q , s 是正整数, a , b , c 是晶格常数。
晶体结构
r 是原子半径
| 参数 | 简单立方晶胞 | 体心立方晶胞 | 面心立方晶胞 | 金刚石晶胞 |
|---|
| 晶胞边长 | 2r | 34r | 22r | 38r |
| 配位数 | 6 | 8 | 12 注意 | 4 |
| 单个晶胞中的原子个数 | 1 | 2 | 4 | 8 |
| 密排指数 | 6π=52% | 83π=68% | 62π=74% | 163π=34%(注意并不是最高) |
| 六方最密堆积的配位数也是 12 ,密排指数同样为 74% 。 | | | | |
密勒指数
晶向和晶面都有密勒指数。
- 晶向:描述晶体内部的一个方向:分解矢量。
- 晶向:[hkl],如果为负数要写为 h
- 等价晶向:<hkl>
- 晶面:描述晶体内部的一个平面:截距→倒数→取最小公倍数
- 晶面:(hkl),负数同上
- 等价晶面:{hkl}
- 特性
- 互质
- 都是整数
- 立方晶体:晶面和晶向的垂直面密勒指数相同
- 其他晶体:若晶面和晶向密勒指数相同,晶向/晶面满足矢量分解/合成的关系。
- 对称性
- 是否能把晶向/晶面转化为等价晶面/晶向与空间晶格的对称性有关
- 简单立方晶体:由于对称性,八种晶向可以等价为 <111> 。
- 1A˚=10−8cm=10−10m
- 原子面密度
面密度=每晶面的面积每晶面的原子数
量子物理
高数知识Recall
- 对于形如 y′′+y′p+qy=0 的微分方程,直接解特征根方程 r2+rp+q=0 ,解得 y=C1er1x+C2er2x
相关参数
- h 普朗克常数,h=6.625×10−34J⋅s
- hwˉ 约化普朗克常数, hwˉ=2πh=1.054×10−34J⋅s
- m0=9.1×10−31kg ,电子质量
- q=1.6×10−19C ,电子电荷
- ϵ0=8.85×10−12F/m ,真空介电常数
- 1eV=1.6×10−19J ,一个电子伏特
基本原理
能量量子化
E=hν
T=21mv2=hν−hν0
其中 hν0 为�逸出功。
- 光电效应
- 高频率的光→更高能量的电子
- 光强大的光→发射更多电子
波粒二象性与物质波
p=λh=hwˉk
(其中:k=λ2π )
E=hν=hwˉw
(其中:w=2πν )
不确定原理
ΔpΔx≥2hwˉ
ΔEΔt≥2hwˉ
薛定谔方程
2m−ℏ2⋅∂x2∂2Ψ(x,t)+V(x)Ψ(x,t)=jℏ∂t∂Ψ(x,t)
其中 Ψ(x,t) 是一个复值函数,是孤立系统量子态的数学表示。
- 令波函数 Ψ(x,t)=ψ(x)ϕ(t) ,可以将薛定谔波动方程化为一边为 x 的函数,一边为 t 的函数的形式,并通过设出 E 这个参量求得 ϕ(t)=e−jwt 。则薛定谔波动方程可以被简化为:
∂x2∂2ψ(x)+ℏ22m(E−V(x))ψ(x)=0
- 由于平方可以消去函数中的复数值,故而将其平方,可以得到与时间无关的 ∣Ψ(x,t)∣2 ,也即概率密度函数, 其中 ∣Ψ(x,t)∣2dx 表示在 t 时刻, x 到 dx 位置找到粒子的概率。
- 波函数归一化条件
∫−∞∞∣Ψ(x)∣2dx=1
- 概率密度的条件
- 根据概率密度的定义, ψ(x) ==有限==、==单值==
- 如果粒子总能量 E 和势函数 V(x) 在任何位置==均为有限值==,则二阶函数必须有限,做那一点的泰勒展开,可以得出==一阶导数连�续==。由于一阶导数跟粒子动量有关,也必须==有限单值==,从而得出函数==连续==
- 如果势函数 V(x) 在某处是无限值,由于上面的推导,可以知道一阶导数不一定连续。
薛定谔方程的应用
自由空间的电子
- 条件 V(x)=0
- 解微分方程∂x2∂2ψ(x)+ℏ22mEψ(x)=0 ,得 ψ(x)=Aejkx+Be−jkx 。我们使用这种形式的解(行波解)是因为它在自由空间中。 ^977c93
- 其中:k=hwˉ22mE 称为波数, 由于 2mE=p2 ,于是有 k=hwˉp 。此处可以联动前面 [[#波粒二象性与物质波) 的内容。
- 代入时间方程:Ψ(x,t)=Aej(kx−wt)+Be−j(kx+wt) ,表现为一个方向为 +x 的波和一个方向为 −x 的波的和。
- 其中, A / B 的值可以通过边界条件确定。
- 如果有一个沿 +x 方向运动的电子,则 B=0 ,此时概率密度函数是一个常量,物理意义是:有明确动量定义的自由粒子在空间任意位置出现的概率相等。
无限深势阱
- 由薛定谔方程可知,如果 E 有限,在 V 为无限的区域, ψ(x) 必须为 0 。
- 在 V 为 0 的区域,同自由空间的电子,可以解微分方程。然而此时粒子处于束缚态,所以解的形式需要写成驻波解: ψ(x)=A1coskx+A2sinkx ,其中 A1 / A2 为复数。 ^916c31
- 考虑薛定谔方程概率密度条件:
- 在边界( x=0 与 x=a )位置波函数必须连续:ψ(x=0)=ψ(x=a)=0
- A1=0
- ka=nπ 时成立,其中参数 n 为正整数(负数不考虑,在求概率密度的时候,实际与正整数相同)
- 考虑归一化条件 ∫0aA22sin2kxdx=1 ,解得 A2=a2
- 得到:ψ(x)=a2sin(anπx) ,其中 n 为正整数。
- 由于 k 的值需满足 k=hwˉ22mE 以及 k=anπ 两个条件,联立可得粒子的总能量
ψ(x)=a2sinknx
由于 kn 必须是分立值,相应的总能量也只能是分立值。这里就体现了量子力学中能量的量子化。
阶跃势函数
- 粒子流入射至阶跃势垒,流动方向为 +x ,起始点 −∞ 。粒子的总能量小于势垒的高度 E<V0
- 在 V=0 的区域,方程的通解为 ψ1(x)=A1ejk1x+B1e−jk1x
- 在势函数 V=V0 的区域,假设 E<V0 ,则有 ψ2(x)=A2e−k2x+B2e+k2x (注意这里e指数上是没有虚数标记的,原因是 E<V0 。) 其中 k2=hwˉ22m(V0−E) 。
- 边界条件:
- ψ2(x) 必须保持有限, B2=0
- 在 x=0 处保持连续, ψ1(0)=ψ2(0)
- 势函数有限——波函数的一阶导 ∂x∂ψ1x=0=∂x∂ψ2x=0 连续
- 解得系数:
B1=k22+k12−(k22+2jk1k2−k12)⋅A1
A2=k22+k122k1(k1−jk2 )⋅A1
- 驻波的概率密度函数同样是取共轭相乘。例如,入射粒子流的流量 vi⋅A1⋅A1∗ ,反射粒子流的流量 vr⋅B1⋅B1∗ 。
- 由 k1=hwˉ22mE 以及 E=21mv2 可得(此时由于 V(x)=0 粒子的总能量与动能相等), vi=mhwˉ2⋅k1 ,也可以知道 vr=mhwˉ2⋅k1 (我觉得是从第二项得到的,方法同上,因为二者的 k 都是 k1 )
- 由此可以得到反射系数 R=ν1⋅A1⋅A1∗νr⋅B1⋅B1∗ 为 1.0
- 存在有限概率的粒子穿越势垒,但最后粒子会完全返回到势垒为 0 的区域中。
矩形势垒
- 同样是 E<V0 的情况,则三个薛定谔方程的解为
- ψ1(x)=A1ejk1x+B1e−jk1x
- ψ2(x)=A2ek2x+B2e−k2x
- ψ3(x)=A3ejk1x+B3e−jk1x
- k1=hwˉ22mE
- k2=hwˉ22m(V0−E)
- 边界条件:
- 连续:x=0 和 x=a 处连续
- 一阶导数连续
- B3=0 因为在那个区域没有反射的粒子
- 透射系数:
T=νi⋅A1⋅Ai∗νt⋅A3⋅A3∗=A1⋅A1∗A3⋅A3∗
- 当 E≪V0 时,T≈16(V0E)(1−V0E)e−2k2a
- 存在有限概率穿过势垒到达对面的区域。
单电子原子
∇2ψ(r,θ,ϕ)+ℏ22m0(E−V(r))ψ(r,θ,ϕ)=0
r21⋅∂r∂(r2∂r∂ψ)+r2sin2θ1⋅∂ϕ2∂2ψ+r2sinθ1⋅∂θ∂(sinθ⋅∂θ∂ψ)+ℏ22m0(E−V(r))ψ=0
- 就像前面解一维形式的薛定谔方程一样:ψ(r,θ,ϕ)=R(r)⋅Θ(θ)⋅Φ(ϕ) ,同样可以看到第二项仅是 ϕ 的函数,同样令第二项为 −m2 ,可以解得 Φ=ejmϕ 。我们知道,在球坐标系中, ϕ 是表示极角的量。ϕ 可以取任意大于 2π 的值,但对于一个球坐标系,相同的角度只能有一个函数值。因而为了保证波函数的单值性, m 需要是整数。我们把 m 称为==量子数==。
- 势函数
V(r)=−4πϵ0re2
- 继续解薛定谔方程,可以得出:
- 主量子数:n=1,2,3…
- 角量子数:l=n−1,n−2,…,0
- 磁量子数:∣m∣=l,l−1,…,0
- 电子的能量(其中 n 是能量量子数/轨道数)
En=(4πϵ0)22ℏ2n2−m0e4=−n213.6eV
来源于对方程
rm0v2=4πϵ01r2q2
以及方程
L=nℏ=m0vr
的联立,解得
r=q2m4πϵ0n2ℏ2
代入 E=Ek+Ep=−214πϵ01rq2 之后解出电子能量。
其中, n 为主量子数。这体现��了能量的量子化。
ψ100=π1⋅(a01)3/2 e−r/a0
其中 a0 为
a0=m0e24πϵ0ℏ2=0.529A˚
将该函数取共轭后与自己相乘,可以得到径向概率密度函数,最大概率出现在半径 r=a0 处。
元素周期表
- 增加了电子的本征角动量(自旋)值为 s=±21 。
载流子模型与特性
- Ec 导带底
- Ev 价带顶
- EG 带隙/禁带宽度
- n 本征半导体内部的载流子数
- p 本征半导体内部的空穴数
- ED 施主态能级(虚线)
- EA 受主态能级(虚线)
- EF 费米能级/费米能量
- k=8.617×10−5eV/K 玻尔兹曼常数
- n0 导带中的电子浓度值
- p0 价带中的电子浓度值
- ni 本征半导体中的电子浓度
- pi 本征半导体中的空穴浓度
- EFi 或 Ei 本征半导体的费米能级(本�征费米能级)
- kT=0.0259eV
载流子模型
价键模型-与空间相关
- 类似于高中化学的模型,硅原子在金刚石晶体中,每个原子与四个最近邻原子相互吸引,形成共价结合。每个原子贡献出四个共享的电子,也接受四个从其他原子共享的电子。
- 一种理想模型
- 在温度接近 0K ,半导体中没有缺陷和杂质原子时,价键模型对半导体的描述是等效的。
能带模型-与能量有关
思想脉络:独立原子→晶体
- 当两个原子距离变近时,原子中电子的势函数相互交叠,于是两个原子互相影响。这种影响使离散的量子化能级分裂为两个分离的能级。下图是一个示意图,参数 r0 代表晶体中平衡原子间的距离。
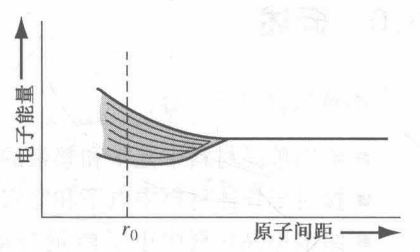
- 分离的能级中,能量仍然是离散的。根据泡利不相容原理,量子数不能改变,故而每个电子须占据独立不同的电子态。由于晶体中的原子所带的电子很多,且允带宽度不大,故而每个能级的间距是很小的,可以认为允带处于准连续能量分布。
- 就硅原子而言,我们在讨论硅的能带时只需考虑 n=3 能级上的价电子,因为剩下两个电子壳层受到核的束缚。 n=3 能级上有俩能量状态, 3s 包括俩量子态, 3p 包含六个量子态。
- 随着原子间距的减小,每个原子的其中 4 个量子态处于较低能带,另外 4 个处于较高能带。 0K 时,电子都处于最低能量状态,较低能带(价带)的所有状态都满,较高能带(导带)的所有状态都空,如下图所示。
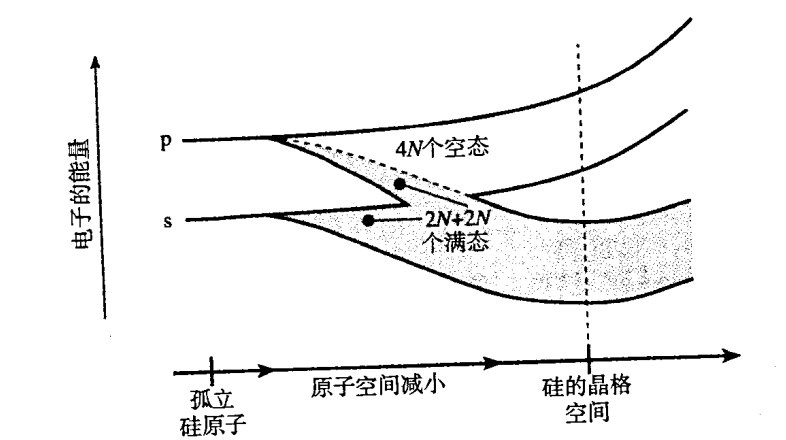
- 我们令 Ec 为最低可能的导带能量, Ev 为最高可能的价带能量, EG=Ec−Ev ,称为带隙的能量。
- 通过克勒尼希-彭尼模型(Neamen那本书3.1.2)解薛定谔方程可以得到粒子能量 E 和对应波数 k 的关系如图所示。
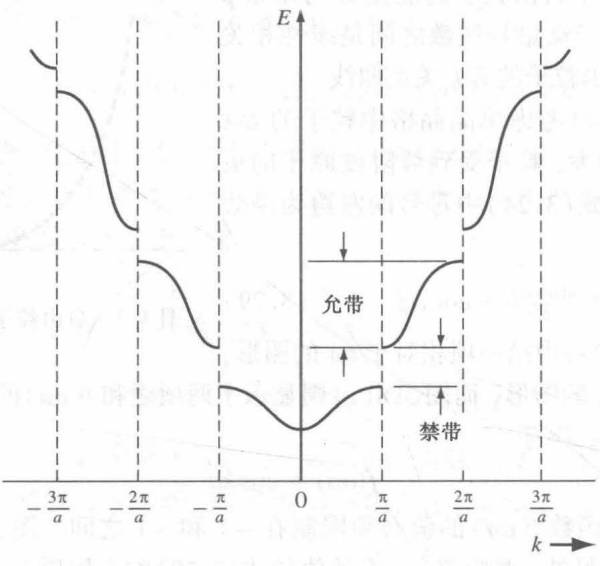 以 2π 为周期进行平移,得到
以 2π 为周期进行平移,得到
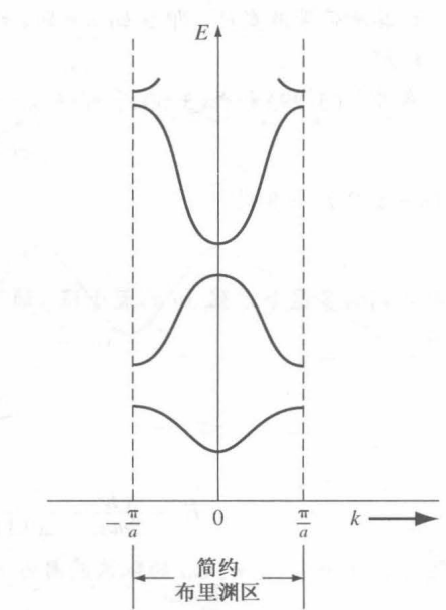
- 基本能带模型图,一条线表示导带中最低的能量,另一条表示价带顶的能量, y 是电子的能量轴, x 方向是位置轴。(如图所示)

能带模型的三维扩展
- 把一维的 E−k 图扩展到三维,k 坐标的变化不仅代表 k 空间的变化,还代表晶向的变化(由于在�特定晶向上, E−k 关系是对称的,故而我们可以在负半轴上画更多的东西),因此,从三维空间的 E−k 关系图上,我们可以看到不同晶向的 E−k 关系。
- 直接带隙半导体:导带最小能量与价带最大能量具有相同的 k 坐标,两个允带之间电子的跃迁不会对动量产生影响。例子: GaAs ,如图所示为砷化镓的能带结构:
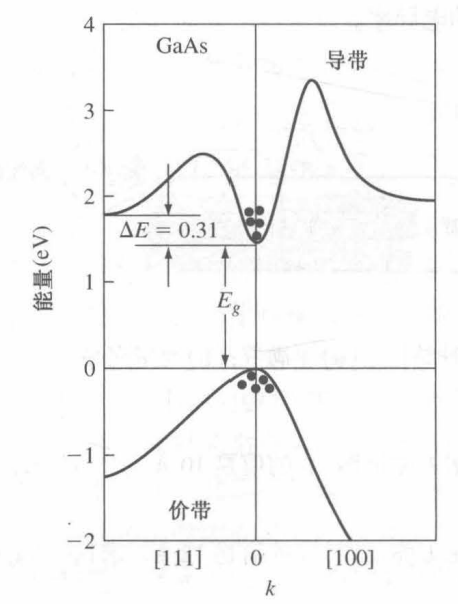
- 间接带隙半导体:价带能量最大值和导带能量最小值的 k 坐标不同的半导体,电子在价带和导带中跃迁时,需要使用动量守恒定律(包含与晶体的相互作用),通过吸收/释放声子的方式对其进行补偿。例子: Si、Ge ,如图所示是硅的能带结构:
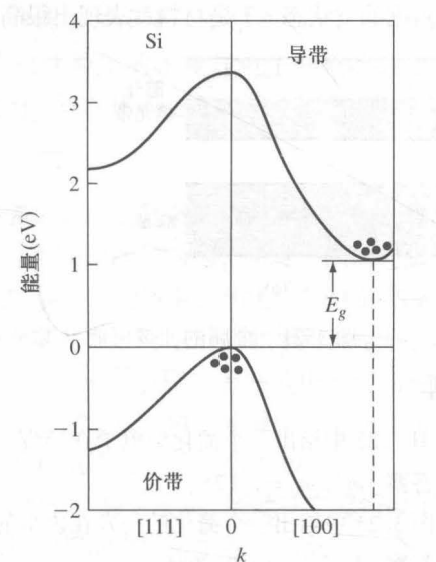
载流子-电流传输的性质
- 电子与空穴倾向于向能级低的地方运动。
- 不存在载流子/电流的情况
- 价键模型没有断裂的键
- 能带模型中价带被电子填满而导带是空的(电子的动量也是量子化的,每个可能的动量状态有一个大小相等、方向相反的动量状态),因为被填满了,所以电子的净动量在能带中恒等于 0 。
- 存在载流子的情况
- 价键模型:出现键的断裂,价电子成为自由电子/载流子
- 能带模型:价带电子受到激发进入导带,产生载流子
- 空穴
- 共价键断裂时,共价键中产生缺键/空位,电子整体的移动造成空位的移动,称为空穴。
带隙与材料分类
| 材料 | 性质 | 能带情况 | 电阻率 |
|---|
| 绝缘体 | 热能只能将很少的电子从价带激发到导带,很难用加热的方法产生电子和空穴,不良导体 | 能带全满或全空,带隙能量 Eg 通常为 3.5∼6eV ,带隙很宽 | ρ=1014∼1018Ω⋅cm |
| 金属 | 良导体,其中有大量的载流子 | 带隙很小,或者是相互重合没有带隙,导带和价带相互重合 | ρ=10−5∼10−6Ω⋅cm ,电阻率随温度升高而升高 |
| 半导体 | 室温下,价带中的一些电子受到激发可以得到足够的热能,到达导带,产生一定数量的载流子 | 带隙介于上述两者之间。近似空带或近似满带,��外加电场可使得电荷运动并产生电流, Eg 通常为 1eV | ρ=10−3∼103Ω⋅cm ,电阻率随温度降低而升高 |
载流子特性
- 电荷粒子:导电电子与空穴;导电电子带负电荷,空穴带正电荷
有效质量
- 电子在晶格中的运动与在自由空间中不同,既受外力影响也受内力影响。因为
很难一一考虑粒子所受的内力,即
Fext=m∗a
m∗ 称为有效质量,概括了粒子的质量以及内力的作用。
- 如何求出粒子的有效质量:
- 从 E=2mp2=2mℏ2k2 开始,之后对 k 求导,得到 dkdE=mℏ2k=mℏp=ℏv ,可知 E 对 k 的一阶导数与粒子速度有关。
- 对 k 求二阶导数:得到 ℏ21dk2d2E=m1 ,我们可以通过这个方程计算有效质量或者判断有效质量的正负。
- 利用有效质量解题
- 对电子而言,运动方程为 F=−qE=mn∗dtdv
- 对空穴而言,运动方程为 F=qE=mp∗dtdv
- 注意电子和空穴之间的区别
载流子数
- 本征半导体:一种半导体材料,杂质含量小于热激发的电子数和空�穴数,或者本征半导体是没有添加其他杂质的天然材料
- 热平衡条件下,半导体内部的本征半导体
n=p=ni
其中硅的 ni 为 1×1010/cm3 。
载流子数的控制(掺杂)
- 施主元素
- 元素周期表中的 V 族元素,多出一个施主电子,不能进入共价键,只能在施主电子周围形成较弱束缚,容易挣脱晶格的束缚,在晶格中自由运动称为载流子。
- 我们可以把施主离子看作氢原子的原子核,而把施主电子看作氢原子的电子,于是可以得到施主电子的结合能 EB≃m0mn∗KS21EH∣n=1≃−0.1eV ,其中 mn∗ 是电子的有效质量, KS=11.8 是硅的介电常数。
- 束缚电子占据的电子能级 ED=Ec−∣EB∣ ( ∣EB∣ 是束缚电子的结合能),能带图如下图
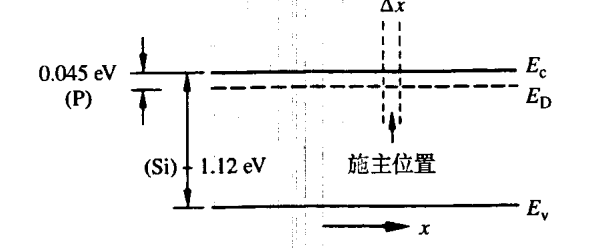 注意这里的能级表现为一组非连续的线,因为束缚电子和施主之间的距离是局域化的,也就是图中 Δx 的范围
注意这里的能级表现为一组非连续的线,因为束缚电子和施主之间的距离是局域化的,也就是图中 Δx 的范围
- 带正电的施主原子不移动
- 不增加空穴的浓度
- 受主元素
- III 族元素,缺少一个电子,需要从临近的硅原子中夺取一个价电子,于是产生一个空穴,称为载流子
- 可以类比施主元素得到受主电子的结合能(使用有效质量与介电常数)与受主能级 EA 。
- 带负电的受主离子不移动
- 不增加电子的浓度
- 施主能级与受主能级在不同温度下的填充效果可以见下图
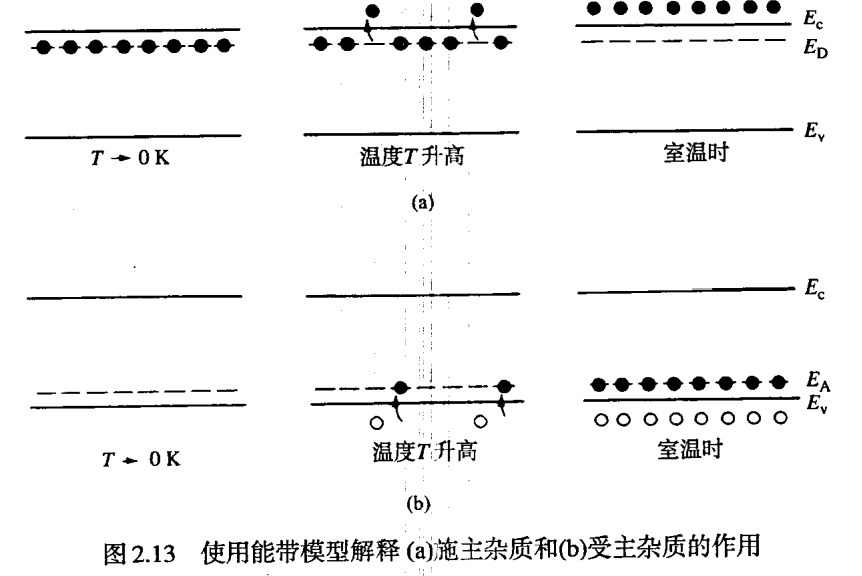
- 非元素半导体的掺杂:类似前述掺杂,施主/受主元素的确定来源于不同元素的施主/受主的状态。
- 如果杂质既有施主的作用又有受主的作用,则称为两性杂质。
相关术语
- 掺杂:为了增加半导体内电子或空穴的浓度,将一定数量的特殊杂质原子掺入到半导体的体内。
- 本征半导体:没有掺杂的半导体;非常纯净的半导体(样品内的杂质原子数量可以忽略不计);具有材料固有性质的半导体。
- 非本征半导体:掺杂半导体;加入的杂质原子控制半导体性质的半导体。
- 施主:能增加电子浓度的杂质原子;n型掺杂。
- 受主:能增加空穴浓度的杂质原子;p型掺杂
- n型材料:掺有施主的材料;半导体内的电子浓度大于空穴浓度。
- p型材料:掺有受主的材料;半导体内的空穴浓度大于电子浓度。
热平衡态下的载流子浓度
- 掺杂半导体内载流子浓度的精确数值
- 掺杂半导体内载流子的分布(是能量的函数)
态密度
- 研究导带/价带中任意给定的能级有多少种状态,单位为 (Numbers of States/cm3)/eV
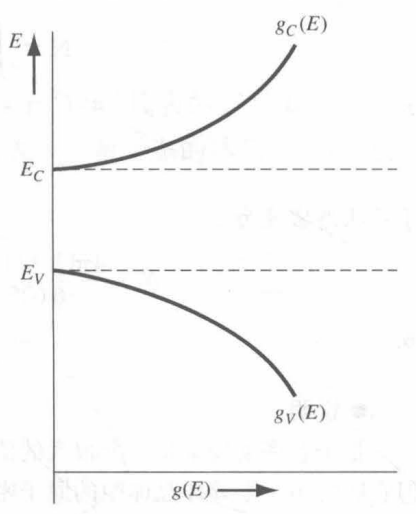
- 当电子能量为 E 且距离带边不远时:
gc(E)=h38π2(mn∗)3/2(E−Ec)forE≥Ec
gv(E)=h38π2(mp∗)3/2(Ev−E)forE≤Ev
or
gc(E)=π2ℏ3mn⋆2mn⋆(E−Ec),E⩾Ecgv(E)=π2ℏ3mp⋆2mp⋆(Ev−E),E⩽Ev
- 物理意义举例: gc(E)dE 描述能量 E 到 E+dE 之间每立方厘米内导带的状态数(条件 E≥Ec )
- 相关图如下图所示
费米分布函数
- 在==热平衡==条件下,求得能量为 E 的状态被电子占据的几率
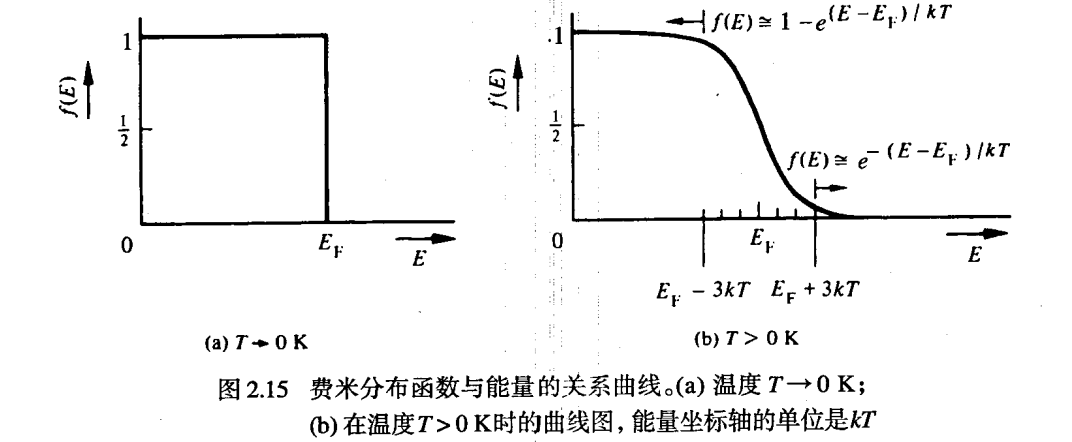
- 费米分布函数 ( T 的单位是 K )
f(E)=1 + e(E−EF)/kT1
- 性质 ^af2f6b
- T→0K
- E<EF ,f(E)→1 ,费米能级之下的量子态全被电子占据
- E>EF ,f(E)→0 ,费米能级之上的量子态几乎全空
- 费米能级是绝对零度时,粒子所能达到的最高能级
- E=EF , f(EF)=21
- E≥EF+3kT , f(E)≃e−(E−EF)/kT ,在费米能级之上 3kT 或者更多的量子态是空的
- E≤EF−3kT ,e(E−EF)/kT≪1 ,因此在费米能级低 3kT 或者更多的量子态几乎是满的。
- 示意图:温度等于/大于 0K 时费米分布函数随能量变化的特性
- 1−fF(E)=1+e(EF−E)/kT1 ,与 fF(E) 关于费米能级对称,也就是 EF 以上 dE 距离处与 EF 以下 dE 距离处空状态的概率相等。
- 联系前面有关施主能级与受主能级的知识,我们可以知道: T=0K 的时候,对于 n 型半导体,费米能级必定高于施主能级;对于 p 型半导体,费米能级必定低于受主能级。
平衡载流子分布
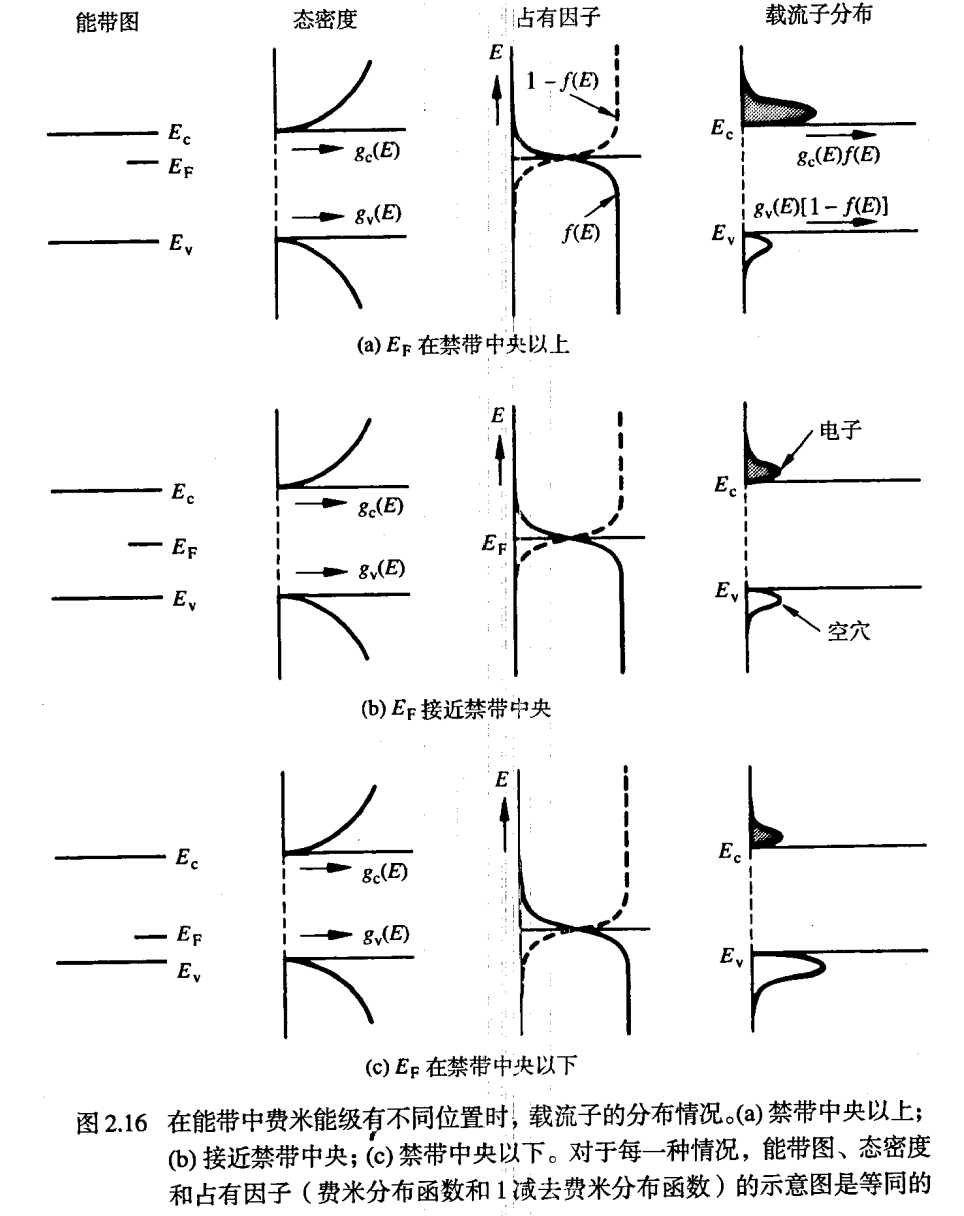
- 不同能带中载流子的分布: 态密度×占有因子
- n=∫EcEtopgc(E)f(E)dE
- 导/价带:导/价带的态密度;
- 电子/空穴:选取相应的占有因子( fF(E) 或者 1−fF(E) )
- 当费米能级处于不同的位置时,载流子的分布情况也不同(注意,下图中的横轴分别为态密度和费米分布函数。
- ==导带电子==的热平衡浓度由上一节的相乘后积分(从导带往上积)以及一堆复杂的数学推导得出(注意: 推导的前提条件是:(Ec−EF)≫3kT ,此时费米概率分布函数简化为玻尔兹曼近似,也即 f(E)≅e−(E−EF)/kT )
n0=Ncexp[kT−(Ec−EF)]
其中: Nc=2(πh22πmn∗kT)3/2 ,是导带的状态密度
- 价带空穴的热平衡浓度,从价带往下积,经过数学推导得出(注意: 推导的前提条件是:(EF−Ev)≫3kT ,此时费米概率分布函数简化为玻尔兹曼近似)
p0=Nvexp[kT−(EF−Ev)].
其中: Nv=2(h22πmp∗kT)3/2 ,是价带的状态密度
- 对比上述两式,有所变化的是不同载流子的有效质量以及导带/价带的顺序,其他没什么变化。
- 从上面的推导条件,我们可以得出简并半导体和非简并半导体的概念:
- 当 Ev+3kT≤EF≤Ec−3kT ,相关载流子的热平衡浓度可以简化成上面的式子,称之为“非简并半导体”(也就是 EF 大概在能带的中间)
- 反之:称为简并半导体。
- 那么,什么时候 EF 离施主/受主能级很近呢?我们考虑杂质浓度增加的情形。
- 如果杂质浓度增加到载流子开始互相作用的程度,分立的施主/受主能级就会分裂成能带,而能带可能与导带底相交叠。
- 如果导带中的电子浓度超过 Nc /价带中的空穴浓度超过 Nv 时,费米能级就位于导带/价带内部(看上面的两个方程)
- 此时材料部分表现金属特性
- 因此,简并半导体/非简并半导体这组概念可以从两个角度来看待:
- EF 也即费米能级的位置
- 半导体中杂质原子的浓度
- 而且上述两个角度是相互关联的
本征半导体
本征载流子浓度
n0p0=ni=Ncexp(kT−(Ec−EEi))=pi=ni=Nvexp(kT−(EEi−Ev))
ni2=NcNvexp[kT−(Ec−Ev)]=NcNvexp[kT−Eg]
or
ni=NcNve−EG/2kT
- T=300K 时,对 Si 而言 ni=1010cm−3
- 影响 ni 的因素:
- T 越大, ni 越大
- Eg 越大, ni 越小
本征费米能级位置
Ncexp[kT−(Ec−EFi)]=Nvexp[kT−(EFi−Ev)]
EFi=21(Ec+Ev)+21kTln(NcNv)
- 将 Nv 与 Nc 代��入:
EFi=21(Ec+Ev)+43kTln(mn∗mp∗)
- 由于电子和空穴的有效质量与状态密度函数相关,因此也跟本征费米能级(电子浓度与空穴浓度相等)有关。但在实际的计算中,上式的后一项因为太小,常常可以忽略。故而有:
Ei=2Ec+Ev+43kTln(mn∗mp∗)≅2Ec+Ev
非本征半导体
载流子浓度
- 我们使用本征半导体的公式推理出 Nc 与 Nv 的表达式,之后把它代入非本征半导体的公式中。因为我们想通过本征求得非本征。(非本征的这些量看上去就不怎么好求的样子)于是有:
NC=nie(Ec−Ei)/kTNV=nie(Ei−Ev)/kT
代入到非本征/一般半导体中:
n=nie(EF−Ei)/kT
p=nie(Ei−EF)/kT
(这两个式子中的 Ei 是本征半导体的费米能级)
pn=ni2
(注意:由于上述式子在推理过程中均使用了玻尔兹曼近似,所以上述公式既适用于本征半导体材料,也适用于非简并的杂质半导体材料)
掺杂浓度与载流子浓度的关系
- 通过热平衡条件我们知道,半导体中不可能存在电场。因为如果存在电场,就会出现载流子的运动,也就不符合热平衡条件的假定了。既然不存在电场,那么半导体中也就没有净电荷。故而我们可以得到==均匀掺杂半导体材料==的内部电中性条件:
p−n+ND+−NA−=0
其中 ND+ 是单位体积内电离施主数, NA− 是单位体积内电离受主数。假设在室温条件下,半导体中受主和施主全部电离,也即:
ND+=NDNA−=NA
于是我们得到
p−n+ND−NA=0
- 将这个方程与 np=ni2 联立,并且解方程,可以得到:
n=2ND−NA+[(2ND−NA)2+ni2]1/2
p=nni2=2NA−ND+[(2NA−ND)2+ni2]1/2
- 性质
- 本征半导体 NA=0 ,ND=0 ,简化为 n=p=ni
- ND−NA≃ND≫ni 或者相反的掺杂半导体。此时 n≃ND ,p=nni2 。
- ni≫∣ND−NA∣ ,当温度升到足够高时,本征激发占主导地位,此时 n≃p≃ni 。在温度足够高,ni≫∣ND−NA∣ 时,所有半导体都将成为本征半导体。
- ND−NA=0 ,类似本征半导体材料,如果 NA 与 ND 二者是可比的但不相等时,这种材料称为补偿半导体,这时不能舍去二者之中的任何一个。
载流子浓度与温度的关系
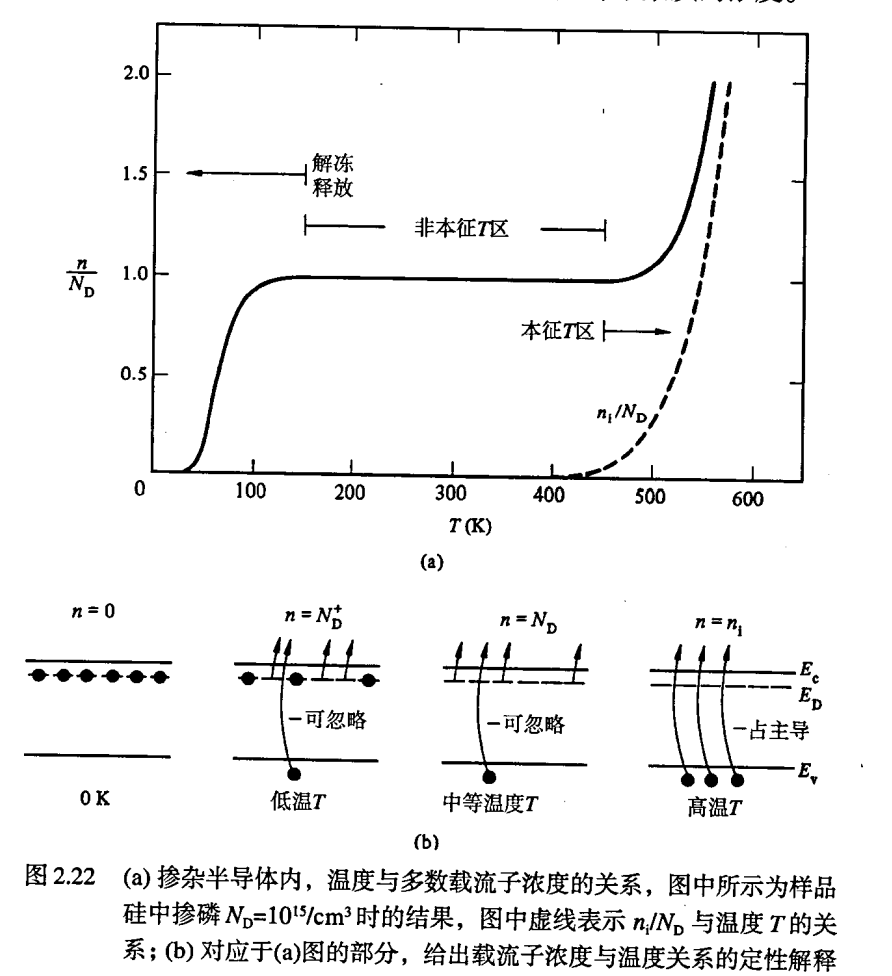
- 两种影响平衡载流子数的机制(以施主掺��杂半导体为例,导带中的电子来自施主电子和价带电子):
- T=0K ,不论是施主电子还是价带电子都无法激发
- 低温 T ,施主电子不断激发
- 中等温度 T ,此时施主状态弱束缚内的全部电子都被释放, n≃ND 并且进入非本征区,此时价带电子不断被激发,但没有达到 ND 的数量级
- 最终电子被激发穿过带隙数达到 ND 的数量级,此时来自施主的电子数基本等于杂质的浓度
- 示意图
费米能级的位置(对于掺杂/非简并/全部电离的半导体)
- 直接通过上面方程解出(这几个量都是知道了其中的一个才能求另一个)
EF−Ei=kTln(n/ni)=−kTln(p/ni)
EF−EiEi−EF=kTln(niND)=kTln(niNA)If ND≫NA,ND≫niIf NA≫ND,NA≫ni
- 在非简并情况下,随着施/受主杂质的增加,费米能级从 Ei 能量有规律地向上/向下移动。如图所示:
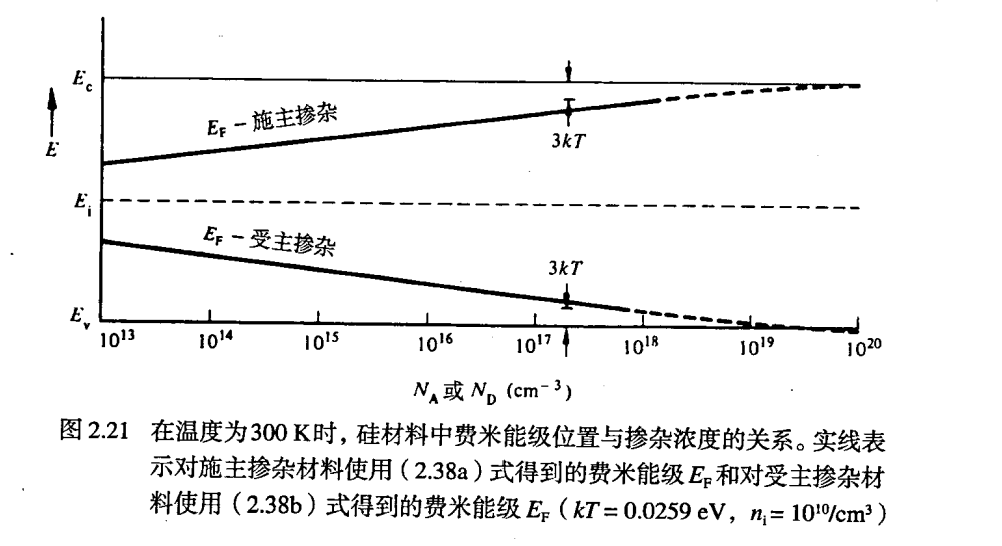
- T 增大, EF 和 Ei 离得越近,因为 T 增大 ni 也增大。
这个费米能级到底TM的是什么东西?
- 费米能级表征了某个能级,比它小的能级大多数被电子填满,而它上面的能级大多数为空。
- 当我们把两块半导体材料放在一起的时候,我们如何判断载流子的浓度呢?通过观察费米能级的大小,我们可以判断载流子的流向。这种载流子的流动以热平衡状态为止。
- 当达到热平衡状态时,两块材料的费米能级相同。
载流子的输运
相关数值:
- 300K 时, qkT=0.0259V
- NT 是 R-G 中心的�数量
能带图与费米能级
- 当我们考虑载流子沿着 x 轴输运的时候,能带能量就变为了位置的函数(能带弯曲)
- 能带图的本质是能带标出了半导体中允许的电子能量与位置的关系。
电子/空穴的动能和势能以及有外电场时能带的弯曲情况
^397caf
- 考虑某个电子吸收能量超过带隙宽度 EG ,则其动能为:E−Ec 。如果把空穴视作电子的反面(也即电子获得动能时,同时产生了一个空穴,二者能量是守恒(?)的),那么空穴的动能就是 Ev−E 。
- 电子的势能: Ec−Eref
- 那么静电势 V 与势能的关系就是: −qV=Ec−Eref (注意这里的负号!)
- 场强则是电势下降的梯度: ε=−dxdV (注意这里的负号!)
- 联立两式,则有:(由于上面那两个式子中的负号可以相互抵消,所以我们可以直接从能带图的斜率近似得到电场和位置的关系)
E=q1dxdEc=q1dxdEv=q1dxdEi
可以这样表示的原因:Ec 、 Ev 和 Ei 之间值相差一个常数。
在扩散情况下费米能级的稳定性
- 如果非均匀掺杂的半导体的平衡条件成立,那么它的费米能级是与位置无关的。
- 更深入地来看,费米能级表征了某个状态被电子占据的几率。在平衡条件下,能量的填充态应该是相同的,否则载流子会在不同几率的状态下迁移,由此产生静电流——这就违反了平衡的条件。
- 下面的示意图是非均匀掺杂半导体的相关能带图像。
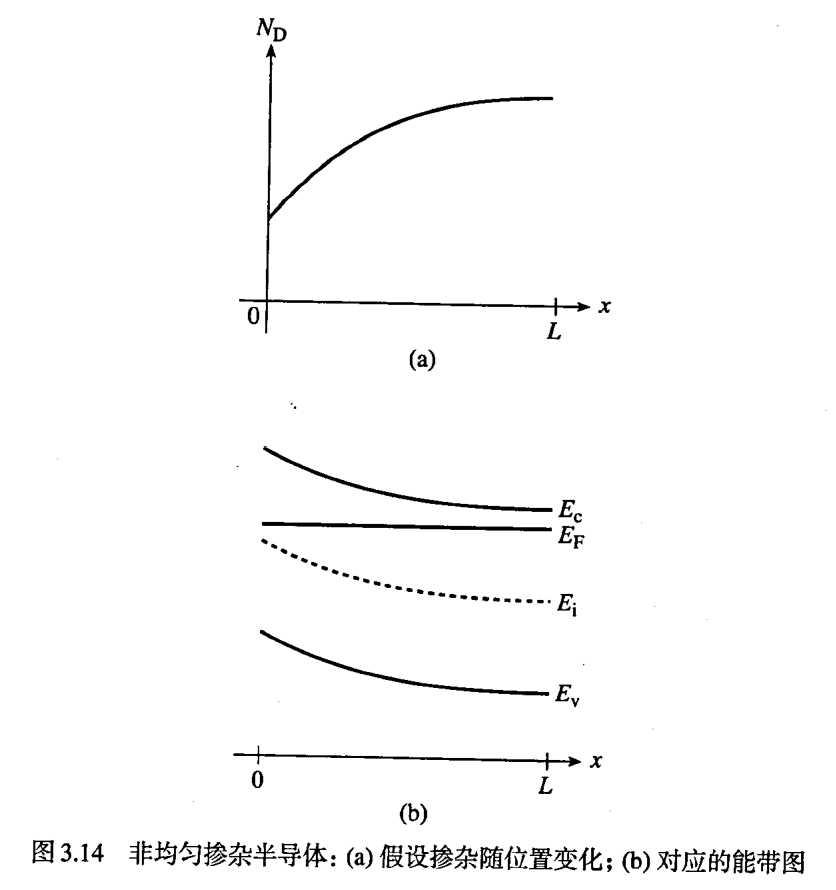
载流子的漂移
- 带电粒子在外电场作用下的运动,并且与电离的杂质原子和热振动的晶格原子不断地与载流子发生碰撞(载流子的加速度不断改变)(当然,还有它本身的热运动)
- 宏观观测到的是固定的漂移速度项( vd )
- 散射机制
- 晶格散射
- 电离杂质(施主/受主)散射
- 晶体中电子与原子的内部场——有效质量
漂移电流
- 漂移电流(单位时间内流过垂直于电流流动方向任意平面的电荷数):
IP∣drift=qpvdA
(以空穴漂移电流为例)
JP∣drift=qpvd
- 可以看出,得到漂移速度跟电场的关系很重要。我们可以得到 vd 跟电场的函数关系。(其中 E 是电场,在硅中,空穴 β≅1,电子 β≅2 )(以空穴漂移电荷为例)
υd=[1+(υsatμ0E)β]1/βμ0E={μ0Eυsatif E→0if E→∞
- 在低电场下,μ0 作为比例常数,同时 vd 与 E 成比例;在高电场下,vd 接近饱和速度 vsat ,漂移电流不显示对电场的依赖性。
- 在低电场中:(以空穴漂移电荷为例)
Jp∣drift=qμppE
电子的漂移电流公式也类似,除了将 p 变成 n 。虽然最终的公式相同,但我们也不能忽略对于电子而言: vd=−μ0E ,并且 JN∣drift=−qnvd 。(扩散电流与电子运动方向相反)
迁移率
- μn 或者 μp ,指移动的自由度,迁移率越高,载流子在半导体内受到的碰撞越少
- 单位 cm2/V⋅s 或者 m2/V⋅s
- 与散射的关系:从动量角度列式 vd=m∗qτE , τ 是两次碰撞的平均自由时间。我们假设低电场,于是有 vd=μ0E ,于是有 μ0=m∗qτ 。
- 与掺杂的关系:对硅而言,在低掺杂浓度下,迁移率与掺杂浓度无关,超过 1015/cm3 ,随掺杂浓度增大而单调减少。
- 与温度的关系:
- 晶格散射/声子散射:与原子的热运动有关。设 μL 是只有晶格散射存在时的迁移率,则有 μL∝T−3/2 。
- 电离杂质散射:与掺杂浓度有关。室温下电子/空穴与电离杂质之间存在库伦作用。引起的碰撞与散射会改变载流子的速度特性。设 μI 是只有电离杂质散射存在时的迁移率。则有 μI∝NIT+3/2
- 温度升高时可能存在的过程
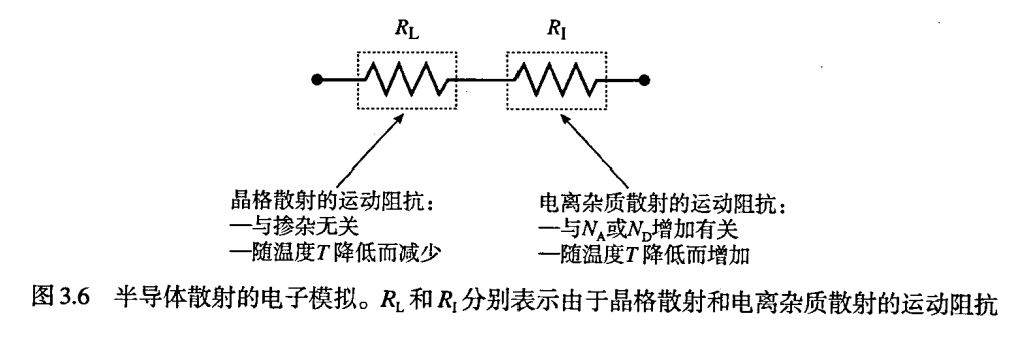
- 低温区:温度升高,电子被电离,浓度上升,迁移率上升
- 中温区(非本征区):温度升高,但杂质已经被完全电离,电子浓度不变。但此时随温度升高晶格散射上升,因此迁移率下降(当然此时电离杂质散射下降,但仍然是晶格散射占主导)
- 高温区:本征载流子浓度增加(见上一章),开始主导电子浓度,随温度升高,迁移率增加。
- 对于高掺杂样品,电离杂质散射比较显著。在低温区,电离杂质散射在全部散射中占的比例较大,因此在这个区域内迁移率与温度的依赖关系的斜率减小。
- 两种散射过程以及迁移率的关系:
- 微分时间 dt 中受到散射的概率:τdt=τIdt+τLdt
- 迁移率(马西森定则): μ1=μI1+μL1
电阻率
- E=ρJ ρ 称为电阻率; J=σE ,σ=ρ1 ,称为电导率。
- 均匀材料中电流密度与电场的关系
Jdrift=JN∣drift+Jp∣drift=q(μnn+μpp)E
ρ=qμnND1…n型半导体
ρ=qμpNA1…p型半导体
测量电阻率
- 四探针法,省去了接触电阻对测量的影响。
- 示意图:
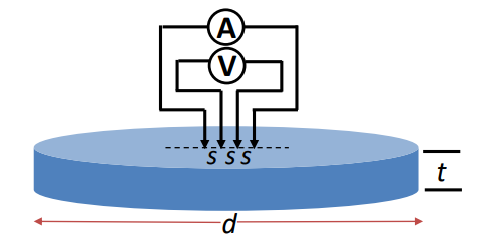
- 相关计算公式
ρ=IV⋅2πs⋅f(d,t)
其中 f(d,t) 称为校正因子。
霍尔效应
- 原理图
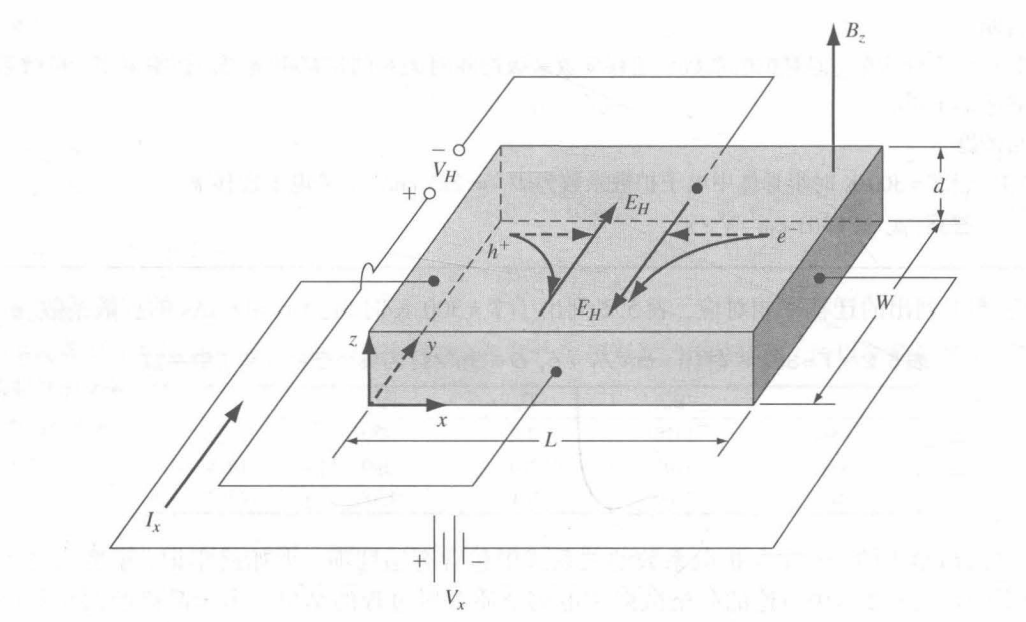 相关公式:
相关公式:
qEy=qvxBz
VH=+EHW
Ey=EH ,于是:
VH=vxWBz
其中, p 型半导体中的空穴漂移速度(注意, n 型半导体中这个式子是有负号的):
vx=qpJx=qp(Wd)Ix
求解霍尔电压 VH 与电流 Ix ,磁场 Bz 的关系:
VH=qpdIxBz
空穴浓度:
p=qdVHIxBz
电子浓度:
n=−qdVHIxBz
求出载流子浓度之后,利用空穴漂移速度 vx=μpEx=μpLVx ,将其代入上面的式子。(条件:弱电场)
得到空穴迁移率:
μp=qpVxWdIxL
电子迁移率:
μn=qnVxWdIxL
载流子的扩散
- 由于无规则的热运动,粒子从浓度高的区域向浓度低的区域在宏观尺度上的移动,结果使得粒子重新分布。
- 扩散与粒子电荷的变化、热运动以及粒子间的斥力无关。
扩散电流
Jn,diff = qDn dxdn
J p,diff = −qDp dxdp
其中 Dn 与 Dp 是电子与空穴的扩散系数,单位是 cm2/s
JP=JP∣drift+JP∣diff
JN=JN∣drift+JN∣diff
J=JN+JP
扩散系数和迁移率的关系
- 前提:在平衡条件下的非均匀掺杂半导体
- 由于是平衡条件,所以总电流为零。又因为半导体是非均匀的,所以此时半导体中存在内建电场,并且内建电场不为零。
- ��我们令:
JN∣dnft+JN∣diff=qμnnE+qDNdxdn=0
我们首先看电场那一项:
E=q1dxdEc=q1dxdEv=q1dxdEi
再代入:n=nie(EF−Ei)/kT , dxdn=−kTnie(EF−Ei)/kTdxdEi=−kTndxdEi 。
将上述两式代入,得到对于电子的爱因斯坦关系式:
μnDN=qkT
对于空穴的
μpDp=qkT
上述关系式在非平衡/非简并状态下也有效。
载流子的产生-复合
- 当半导体的平衡状态受到微扰时,半导体内部的载流子浓度会涨落。复合-产生是一种恢复机制。
- 分析工作时非平衡的器件。
- 二者是一组相关的过程:
- 复合:电子和空穴被湮灭/消失的过程
- 产生:电子/空穴被创建的过程
几种R-G过程
- 直接复合/产��生:导带电子和价带空穴的直接湮灭/电子被激发后,直接从价带进入导带;这个过程会产生过剩的能量释放/吸收热能或者光能

- 间接复合/产生(R-G中心复合/产生):通过中介物进行的复合过程,只在半导体内复合中心(晶格缺陷/特殊的杂质原子,相比受主和施主浓度很低)的特殊位置产生。在靠近带隙中心引入了允许电子能级 ET ,不同杂质产生的能级不尽相同。
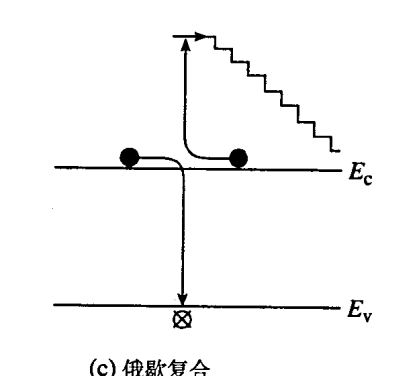
 复合:首先一种载流子漂移进入R-G中心附近,被相关势阱捕获,失去能量;之后出现另一种载流子,二者互相吸引,失去能量,在中心内与电子一同湮灭。也有可能,电子失去能量后,在价带与空穴一起湮灭。产生过程也类似,热能作为中间媒介,在R-G中心产生载流子。
复合:首先一种载流子漂移进入R-G中心附近,被相关势阱捕获,失去能量;之后出现另一种载流子,二者互相吸引,失去能量,在中心内与电子一同湮灭。也有可能,电子失去能量后,在价带与空穴一起湮灭。产生过程也类似,热能作为中间媒介,在R-G中心产生载流子。
- 俄歇过程:两个同种类型的载流子发生碰撞,发生直接复合,释放的能量传递给经过碰撞保存下来的那个,后者与晶格碰撞失去能量,并产生热量。
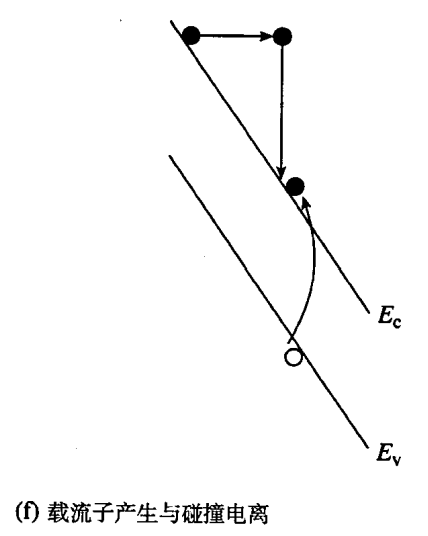
- 碰撞电离:高能载流子与晶格碰撞,释放能量并产生一对电子和空穴。(常常在外电场 E 比较大的地方产生)
不同R-G过程在不同半导体中是否占据主导
- 直接/间接R-G过程:室温下非简并掺杂半导体的低 E 区域
- 发射光子:能量+很少量的动量,光助跃迁在 E−k 图中基本垂直
- 发射声子:很少量的能量+动量,声助跃迁在 E−k 图中基本水平
- 直接带隙半导体:产生/复合时,能量变化+很小的动量变化
- 间接带隙半导体:产生/复合时,�能量变化+较大的动量变化
- 在直接带隙半导体中,直接复合以很快的速度产生。
- 所以,如果在间接带隙半导体中进行直接复合,必须伴有声子+光子的吸收与发射。事实上,间接带隙半导体中,R-G中心复合(间接复合)机制是主要的复合过程。
- 俄歇复合:器件结构的高掺杂区域
- 碰撞电离:器件的高 E 区域
对R-G过程的数学描述
光产生
∂t∂nlight=∂t∂plight= GL(x,λ)
GL 光产生率:(1个/cm3⋅s)
GL(x,λ)=GL0e−αx
GL0 是 x=0 处的光产生率,α 是吸收系数,与材料和波长有关。
特殊情况下的R-G过程(间接热复合-产生)
- 产生的微扰必须是少数载流子“小注入”
- Δp≪n0 ,且 n≃n0 (在 n 型材料内)
- Δn≪p0 ,且 p≃p0 (在 p 型材料内)
- 注意,其中少数载流子可以比平衡浓度下的少数载流子的浓度高。
- 考虑 R-G 过程下的小注入导致的微扰的过剩导致的少数载流子的湮灭
- 由于是小注入,少数载流子远小于多数载流子,所以电子总能迅速到 R-G 能级上与空穴结合。所以单位时间内少数载流子的变化与 R-G 中心数量 NT 成比例。
- 同时,少数载流子的变化也与少数载流子本身的浓度成比例。
- 引入比例常数 cp
- 考虑到少数载流子不断减小,所以在公式前面加负号。
- 故有公式:∂t∂pR=−cpNTp
- 考虑少数载流子的产生
- 在实验上这个数量只与R-G中心的数量有关。
- 故有公式:∂t∂pG=cpNTp0
- 两者相加:
n 型材料中的空穴:
∂t∂pR−Gi−thermal= −cpNTΔp
p 型材料中的电子:
∂t∂nR−Gi i−thermal = − cnN TΔn
τp=cpNT1
τn=cnNT1
∂t∂pR−Gi−thermal=−τpΔp
∂t∂nR−Gi−thermal=−τnΔn
∂t∂pR−G=∂t∂nR−G=−τp(n+n1)+τn(p+p1)ni2−np
其中
n1=niexp[(ET−Ei)/kT]p1=niexp[(Ei−ET)/kT]
少子寿命
- τn 和 τp 是少数载流子的平均寿命,也就是:少数载流子在多子海洋中存活的平均时间。
- 寿命测量:时域光电导,连一块半导体到电路里,照光,测电导的变化
υL≡2VA(1+σdarkΔσ)=VL+υ0e−t/τp
后者是瞬态衰减项。
状态方程
∂t∂n=∂t∂ndrift+∂t∂ndiff+∂t∂nR−Gthermal+∂t∂n(light.etc)other
∂t∂p=∂t∂pdrift+∂t∂pdiff+∂t∂pR−Gthermal+∂t∂p(light.etc)other
代入后有:
∂t∂n=q1∂x∂Jn(x)−τnΔn+GL
∂t∂p=−q1∂x∂Jp(x)−τpΔp+GL
少子扩散方程
- 条件
- 一维
- 少子
- 电场约为 0 (舍去漂移项)
- 平衡少子浓度不是位置的函数
- 小注入条件
- 间接热复合-产生(间接带隙半导体)
- 排除光产生
- 少子扩散方程
∂t∂Δnp∂t∂Δpn=DN∂x2∂2Δnp−τnΔnp+GL=Dp∂x2∂2Δpn−τpΔpn��+GL
- 条件与简化
- 稳态: ∂t∂Δnp→0 (∂t∂Δpn→0)
- 无浓度梯度/扩散电流: DN∂x2∂2Δnp→0 (Dp∂x2∂2Δpn→0)
- 无热 R-G 时: τnΔnp→0(τpΔpn→0)
- 无光照时:GL→0 (或瞬时光照)
扩散长度
- �少子在被湮灭前能够在大量多子内扩散的平均距离
- n 型材料的少子空穴
LP=DPτp
LN=DNτn
准费米能级-非平衡态描述载流子浓度
- 将能带图推广到非平衡态,也就是“==非热平衡状态==”
- 非平衡态的非简并半导体:
n≡nie(FN−Ei)/kTp≡nie(Ei−FP)/kT或 FN≡Ei+kTln(nin)或 FP=Ei−kTln(nip)
- 非平衡到平衡态,也就是 FN→EF 且 FP→EF 的过程。
- 准费米能级随位置变化,表示在半导体中有电流流动。
其他输运
PN结的特性
- 基本知识
- P型半导体和N型半导体放在一起的时候,电子/空穴形成扩散,扩散之后形成电场,电场与电子/空穴的扩散作用发生抵消。
- P区与N区的分界线:冶金结
- 两边叫做准中性区,中间叫做耗尽层
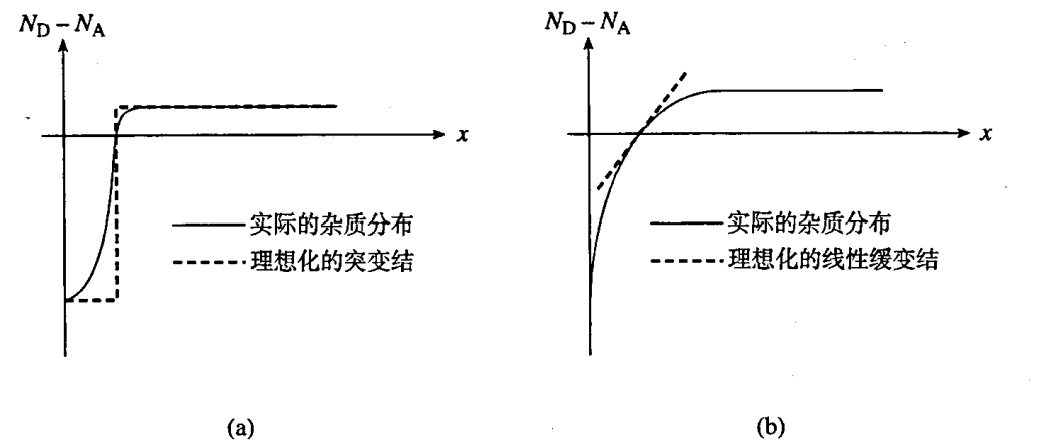
- 杂质分布-净杂质浓��度 ND−NA ,实际工艺具有复杂度,进行理想化处理
- 突变结�分布(离子注入,轻掺杂)
- 线性缓变结分布(中等掺杂,重掺杂)
- 示意图
- 假设
- 玻尔兹曼分布(非简并半导体)推导出不同能级的载流子浓度
- 完全电离(室温下完全电离)
内建电压
- 由于PN结处于热平衡状态,故而半导体的费米能级处处相等,并且是恒定的值。然而P型半导体与N型半导体中,费米能级的位置并不相同。于是,空间电荷区所在位置的导带和价带就要发生弯曲。示意图
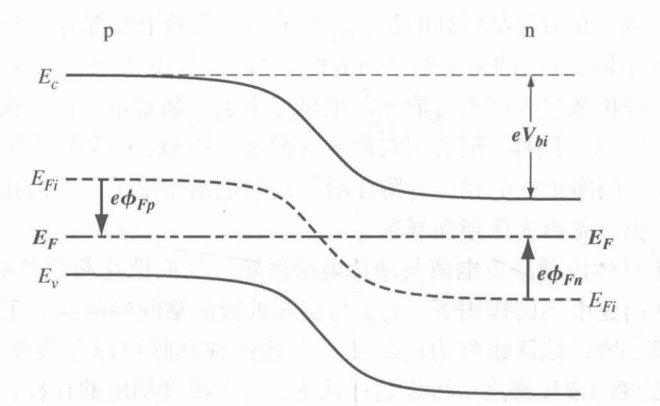
- 内建电势差 Vbi ,维持多子/少子的平衡,故而它在半导体内不产生电流。外加探针与半导体之间也会产生相应的电势差(电子/空穴的运动),故而伏安表无法测出。
- 载流子浓度 → ϕFp 与 ϕFn 的大小 → Vbi 的大小
Vbi=qkTln(ni2NaNd)
其中, Nd 是 n 区的净施主浓度;Na 是 p 区的净受主浓度。
- 另一种计算 Vbi 的方法(利用平衡条件下 J=0 得出)
E=−dxdV
积分: V(xn)−V(−xp)=Vbi
E = −μnDNndn/dx= −qkTndn/dx
Vbi=−∫−xpxnEdx=qkT∫n(−xp)n(xn)ndn=qkTln(n(−xp)n(xn))
- 这个式子相比上式更加普适。上式也是把 xn 与 xp 处的数值代入后得出的。
耗尽近似
dxdE=KSε0ρ=KSε0q(p − n + ND − NA)
- 为了方便地得到 n / p 的值,需要对实际电荷的分布进行理想化近似
- 冶金结附近( −xp≤x≤xn ),与杂质浓度相比,载流子浓度近似忽略不计
- 耗尽区之外的电荷密度处处为 0
- 对于一维突变结,引入耗尽近似,电荷密度:
(注意,下面的积分也要用耗尽近似:也即 E(−xp) 与 E(xn) 均为 0 )
ρ=⎩⎨⎧−qNAqND0if −xp≤x≤0if 0≤x≤xnif x≤−xp or x≥xn
两边分别积分:
E(x)=−KSε0qNA(xp+x)...−xp⩽x⩽0
E(x)=−KSε0qND(xn−x):...0≤x⩽xn
- 在 x=0 处电场连续: qNAxp=qNDxn
- 通过 E=−dV/dx ,可以有方程(注意上下界的选取)
dxdV=⎩⎨⎧KSε0qNA(xp+x)KSε0qND(xn−x)...−xp⩽x⩽0..0⩽x⩽xn
V=0atx=−xpV=Vpiatx=xn
V(x)=2KSε0qNA(xp+x)2 . ...−xp⩽x⩽0
V(x)=Vbi−2KSε0qND(xn−x)2..0⩽x⩽xn
- 令 V(0) 相等,并且使用上面的电荷守恒的条件,可以推出 xp 与 xn ,以及 W=xn+xp 的值
W≡xn+xp=[q2Ksε0(NANDNA+ND)Vbi]1/2
其中:
xp=NA+NDNDW
xn=NA+NDNAW
偏置电压下的PN结
- 对于小电流注入,接触电极到耗尽层边界的准中性区上电阻压降忽略不计。电压压降在耗尽层上。
- 设正偏电压为 VA ,耗尽层的电压为: Vbi−VA (可以把整个电路看作两个电源)
- 我们可以根据上面的推论对零偏时的电场、电压与耗尽层的长度进行修正。
对 0≤x≤xn :
V(x) = Vbi − VA − 2KSε0qND(xn − x)2
W=[q2KSε0(NANDNA + ND)(Vbi − VA)]1/2
前提:VA≤Vbi ,当 VA 趋近 Vbi 的时候,不能忽略准中性区的压降。
- 结果分析:
- VA>0 耗尽层宽度减少,结内电荷减少,电场降低,电势减少。
- VA<0 耗尽层宽度增大,结内电荷增多,电场增大,电势增大。
- 费米能带图:
由上面的推测,可以得到
EFp−EFn=−qVA
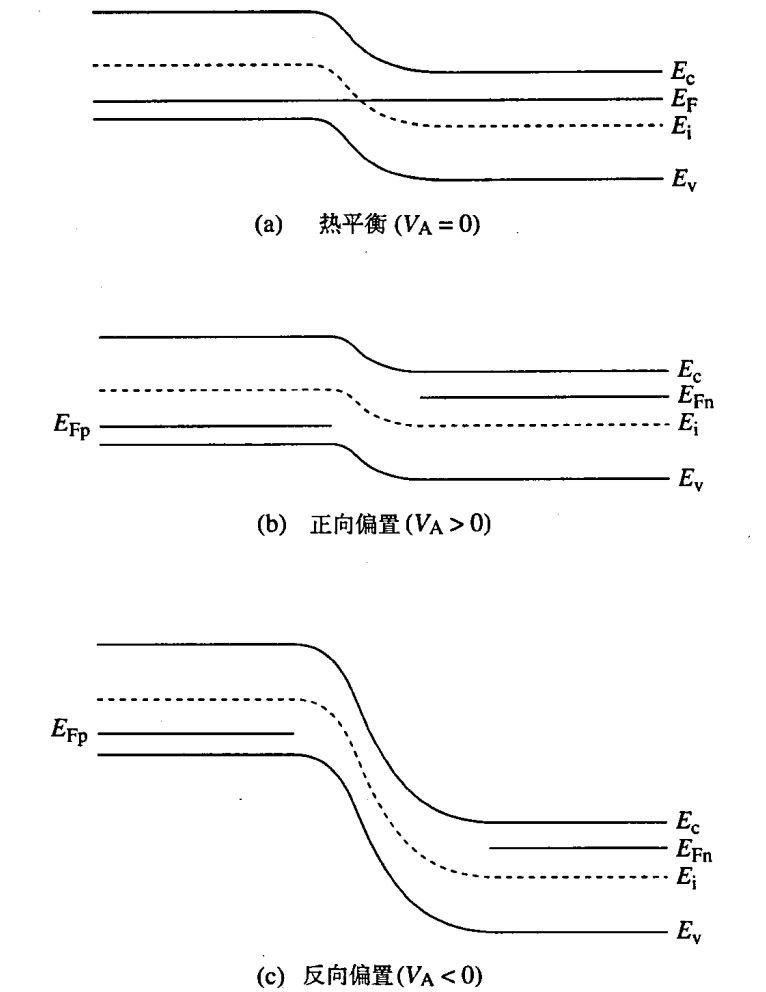
PN结的I-V特性
- V=0 时,载流子通过扩散,只有较高能量的电子可以克服势垒,进入结的另一侧。而另一侧,少数载流子进入耗尽层后,却会被电场很快地扫到结的另一侧。平衡时:对电子而言: p 型到 n 型的漂移电流抵消 n 型到 p 型的扩散电流。
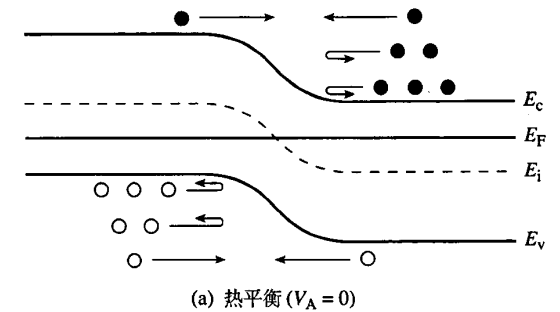
- VA>0 ,势垒出现下降,更多载流子可以通过扩散的形式到耗尽层的另外一侧,导致电流 I=IN+IP (电子电流+空穴电流)。
- 示意图:
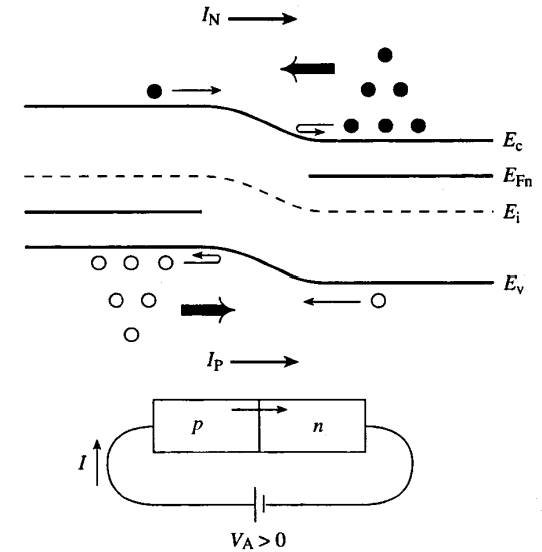
- 外加电压和电流的关系:外加电压与能级变化成线性,能级变化与载流子浓度成指数关系,而载流子浓度又与电流有线性关系,所以外加电压与电流呈指数关系。
- 注入的载流子如何湮灭:多子扩散到耗尽层的另外一侧后,借助复合-产生中心发生复合。
- VA<0 ,势垒上升,载流子很难通过扩散越过势垒,而少数载流子更容易经由电场通过耗尽区到对面的准中性区。因此此时,反向偏置电流与少数载流子有关,且非常小。
- 示意图:
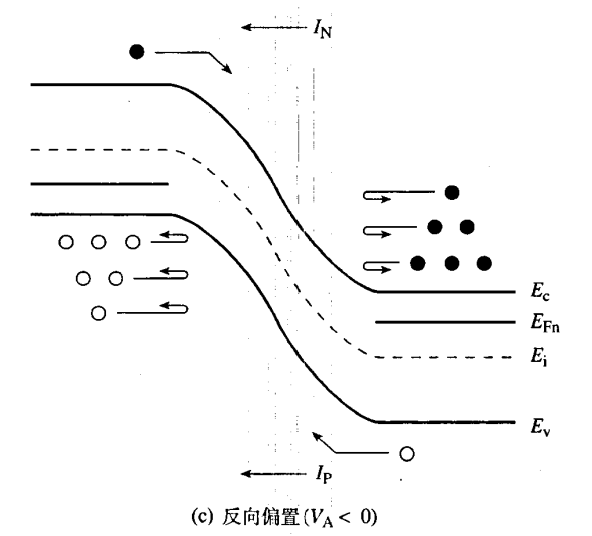
- 外加电压与电流的关系:少数载流子的漂移电流不受势垒高度的影响。与电流大小有关的是每秒进入耗尽层的少数载流子数目。
- 注入和抽取的载流子如何得到补充:少子进入耗尽层后,借助复合-产生中心产生出的载流子会替代离开的载流子。而过剩的多数载流子会导致一个局部电场,将载流子推向接触电极,使得多余的载流子进入外部电路。
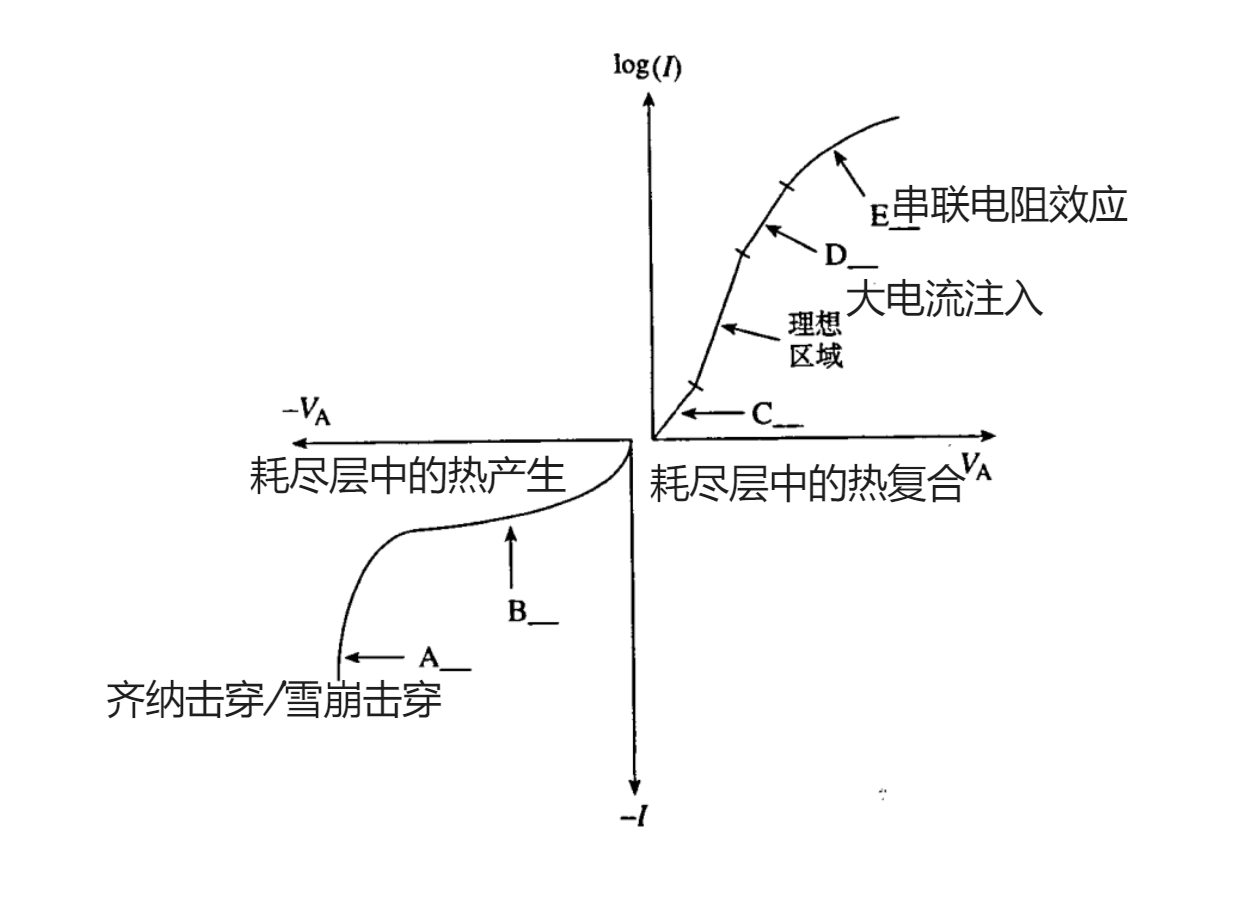
- 由上述推理,得到 I−V 关系的通用形式:
I=I0(eVA/Vref−1)
或者
I=I0(eqVA/kT−1)
定量求解
- 二极管在稳态
- 非简并掺杂,突变结
- 一维
- 准中性区域,小电流注入
- GL=0 ,二极管内除去漂移/扩散/热复合-产生之外没有其他过程。
- 二极管的准中性区满足少数载流子扩散方程的假设条件, E≅0 和小电流注入。
耗尽层
- 假设:耗尽层内载流子没有热复合-产生过程。于是代入连续性方程,有:
dxdJN=dxdJP=0
也即:耗尽层中的 JN 与 JP 为常数。可以得到
J=JN(−xp)+Jp(xn)
准中性区
- 由于有假设:稳态/ GL=0 ,于是有少数载流子扩散方程:
0=DNdx2d2Δnp−τnΔnp x⩽−xp0=Dpdx2d2Δpn−τpΔpn x⩾xn
- 由于有假设: E≅0 以及 dxdn0=dxdp0=0 。则在中性区的载流子电流密度可以化简为
JN=qDNdxdΔnpJp=−qDpdxdΔpn..x⩽−xp...x⩾xn
- 边界条件:“宽基层”二极管,二极管的接触电极与耗尽层边界之间的距离是少数载流子扩散长度的几倍或更多。
Δnp(x→−∞)=0
Δpp(x→+∞)=0
- 边界条件:考虑耗尽层边界,并认为边界处准费米能级与 p / n 区域的费米能级等同(FN−FP=qVA),由准费米能级的两个式子,可以得出PN结定律
np=ni2eqVA/kT...−xp⩽x⩽xn
由此可以得出:
Δnp(−xp)=NAni2(eqVA/kT−1)
Δpn(xn)=NDni2(eqVA/kT−1)
(注意是 Δpn 哦,不是 pn )
- 将边界条件代入到准中性区的少数载流子扩散方程,同时设定新的坐标系如图:
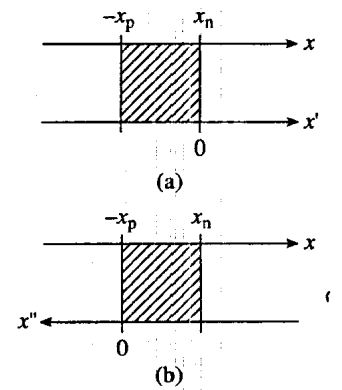
- 可以得到:
Δpn(x′)=NDni2(eqVA/kT−1)e−x′/LP
Δnp(x′′)=NAni2(eqVA/kT−1)e−x′/LN
- 这里也可以严格推导出PN结定律,并求出 I0 的值
I0≡qA(LNDNNAni2+LP��DPNDni2)
(注意:在计算这个值的时候,仅需要考虑轻掺杂一侧)
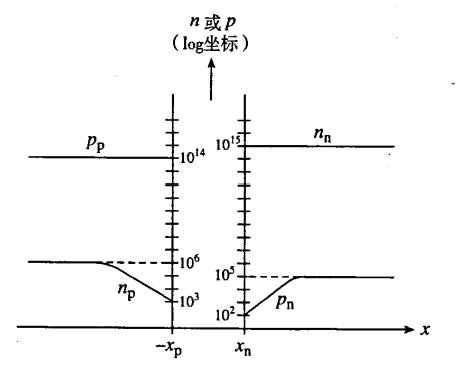
- 少数载流子扩散电流:在准中性区,电流随着距离耗尽层边界处的距离加大而衰减。(正向偏置)
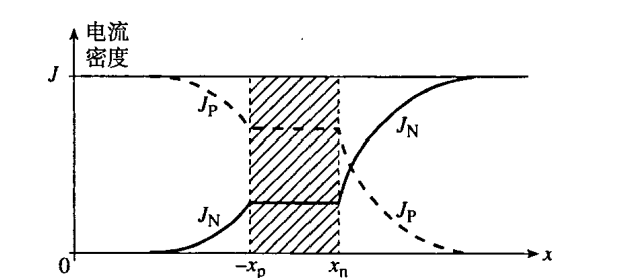
- 载流子浓度:
- 正偏时,少数载流子浓度高于其对应的热平衡值,随着与耗尽层边界的距离的增加,非平衡载流子浓度呈指数形式衰减,在无限远处回归其平衡值。示意图
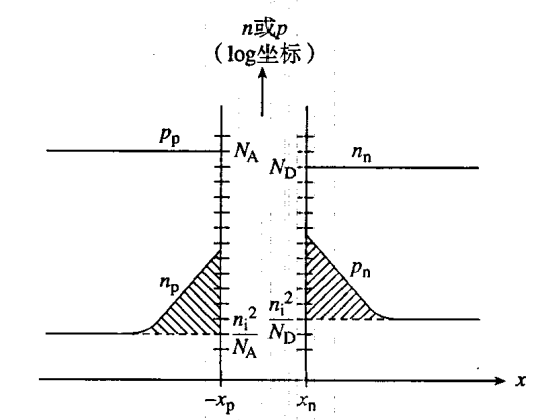
- 反偏时,少数载流子浓度低于其平衡值,其余同上。
与理想情况的误差
假设的打破:没有其他过程——反向击穿
- 击穿是可逆的
- 击穿电压:(对于单边结), x=0 处的电场( ECR )为 Ksϵ02q(Vbi−VA)N 。如果反偏电压超过了某个特定的值(反偏电压 VBR ),那么PN结就会被击穿。相关公式
ECR = Ksϵ02qN(Vbi + VBR)
VBR = 2qNKsε0ECR2−Vbi
- 对单边结而言, N 增大 VBR 降低;带隙宽度越大, VBR 降低。
- 雪崩击穿:穿过耗尽层时,载流子一边加速一边与半导体晶格发生碰撞,并损失能量。当反向偏压不断增加并接近击穿电压时,每次碰撞传递的能量可以使得半导体原子“电离化”。(使原子释放出一个价带电子,产生一个电子-空穴对,称为碰撞电离)额外产生的载流子与原来的载流子一起在耗尽层中加速,产生出更多载流子,反向电流急剧增加至无穷大。在击穿前的几个伏特处,就存在明显的递增现象。
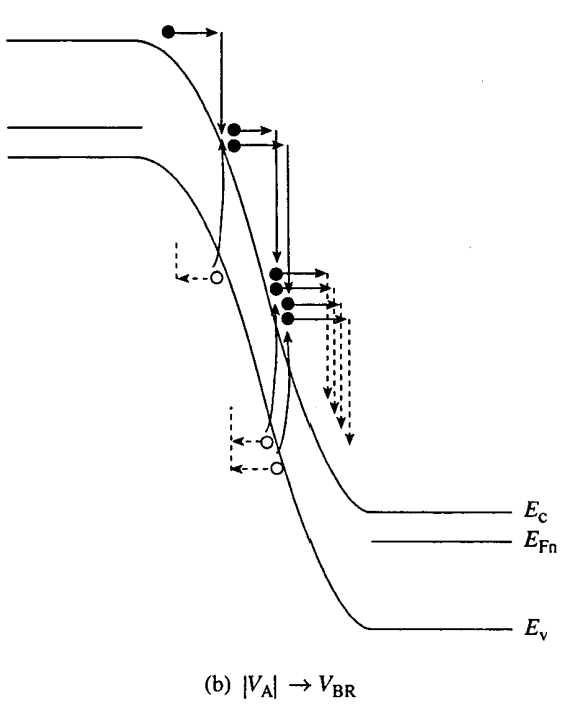
- VBR∝NB1 。
- VBR 会随温度的上升而增加。因为温度上升导致晶格散射的作用增强,平均自由程减小,需要更大能量使雪崩发生。
- 齐纳击穿:反向偏置二极管中出现量子隧穿现象。要求势垒另一侧的能级位置存在着允态,势垒宽度要很薄( <10nm )。
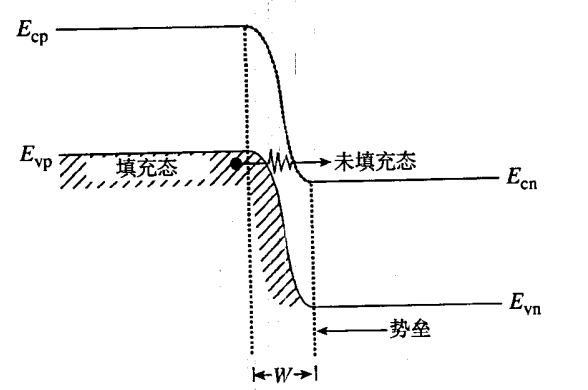
- 结两侧都是重掺杂的二极管中,齐纳过程会比较显著
- 击穿电压 VBR 随温度上升而降低。温度升高,价电子更容易摆脱共价键的束缚,可以隧穿的价带电子增多,因此更容易击穿。
假设的打破:假设价带中有电流的复合-产生
- 在推上面的公式的时候,忽略了耗尽层中的热复合-产生过程。
- 二极管处于反向偏置的时候,耗尽层中载流子浓度会下降,高于其热平衡值(因为其中只有少数载流子),导致耗尽层中电子和空穴的产生,所以反向电流增大
- 二极管处于正向偏置的时候,耗尽层中载流子浓度上升,低于其热平衡值(其中流过多数载流子),导致耗尽层中出现电流的复合,因此正向电流减少。
- 使用R-G过程相关的公式进行计算:
IR−G=qA∫−xpxnτp(n+n1)+τn(p+p1)np−n12dx
- 反向偏压(耗尽区载流子忽略不计,且反向偏压 > 几个 qkT):
IR−G = − 2τ0qAniW
其中:
τ0≡21(τpnin1+τnnip1)=21(τpe(ET−Ei)/kT+τne(Ei−ET)/kT)
- 正向偏压(耗尽区载流子不能忽略不计,正向偏压大于 > 几个 qkT ):
IR−G∝qAniWeqVA/2kT
I=IDIFF+IR−G
- 反向偏压时, VA 越大, W 越大,因此 IR−G 也就越大。
假设的打破:大电流时,准中性区的压降相比耗尽层的压降不能忽略
- 需要考虑准中性区上的压降。因此耗尽层上的压降(结电压 VJ )与 VA 有如下关系
VJ = VA − IRS
- 修正串联电阻的影响:用 VJ 代替 VA
I=I0eqVJ/kT=I0eq(VA−IRS)/kT
- 计算:假设已知 VJ ,可以计算出 I ,之后可以计算出 VA
- 相当于消耗掉了一部分外电压,需要更大的外电压来达到相同的电流。
- 确定串联电阻:
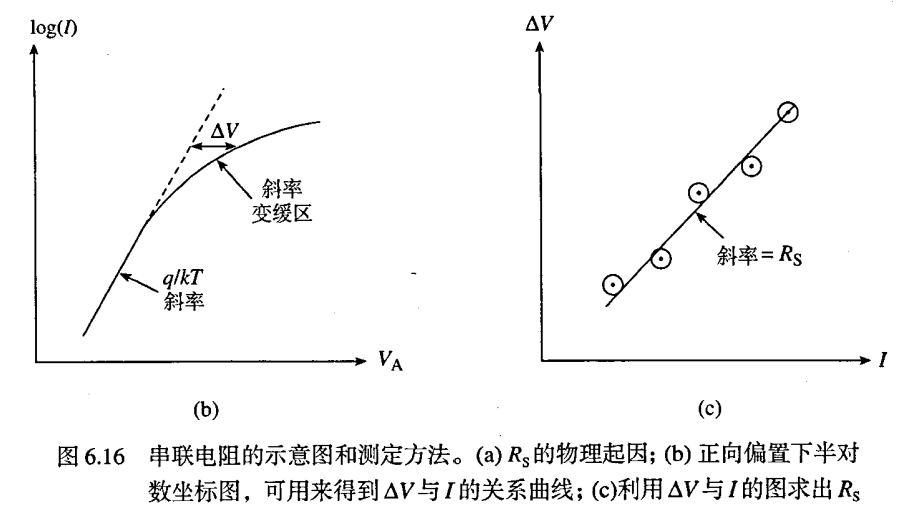
假设的打破:准中性区域边界处有可能不是小电流注入
- 正偏时,当电压很大的时候,耗尽层边界处少数载流子的浓度接近杂质浓度,少数载流子和多数载流子的浓度都出现波动,于是产生了反向电流。
- 室温下,外加电压低于 Vbi 零点几个伏特时出现。
- 示意图:

- 常常与串联电阻效应混同。
电荷控制模型
- 描述准中性区内过剩/不足的少数载流子电荷的行为表达式。
- p+−n 结二极管 n 型一侧的过剩少数载流子:
QP=qA∫xn∞Δpn(x,t)dx
dtdQP= iDIFF− τpQP
- 两种方式可以改变区域的过剩空穴电荷:空穴流入流出/R-G机制。
- 通过上述方式,我们也可以求出准中性区的电流。考虑稳态下: dtdQP=0 ,所以有:
IDIFF=τpQP
IN(−xp)=τn−QN
- 我们可以通过估计 QP 的值简化求出 IDIFF 的步骤。认为 QP 服从长方形分布,于是有:
QP≅q(ALP)Δpn(x′=0)=qALPNDni2(eqVA/kT−1)
IDIFF=τpQP=qAτpLPNDni2(eqVA/kT−1)
窄基区二极管
- 仍然是对前述假设的修正。这里我们考虑准中性区域宽度等于或者小于少数载流子扩散长度的二极管。对于 p+−n 结二极管,有如下的边界条件:
Δpn(x′=0)=NDni2(ekTqVA−1)Δpn(x′=xc′)=0
其他推导同理想二极管,可以解出:
Δpn(x′)=Δpn(0)sinh(Lpxc′)sinh(Lpxc′−x′)
IDIFF=I0′(ekTqVA−1)I0′≡qALPDPNDni2sinh(LPxc′)cosh(LPxc′)
其中:
sinh(x)=2ex−e−x
cosh(x)=2ex+e−x
sinh(ξ)→{ξ2eξ⋯ξ→0⋯ξ→∞
cosh(ξ)→{1+2ξ22eξ⋯ξ→0⋯ξ→∞
- 极限情况:
- xc′→∞ ,该式化简为理想二极管公式
- xc′→0 or LPxc′≪1 ,可以将该式化为: Δpn(x′)=Δpn(0)(1−xc′x′) 这时, Δpn 是一个线性的方程。
- Jp 是一个常数。
- 忽略了热复合-产生项(因为准中性区太短了,可以忽略不计)
- I0′→qA(NDni2)(xc′DP) 。反向偏压升高,耗尽层宽度增加,准中性区域的宽度 xc′=xc−xn 减小。由上面近似的式子可以知道, IDIFF 会随着反向偏压增加而增大。
- xc′→0 的时候,称其为穿通,IDIFF(VA<0)→−∞ 。此时理论公式无效。
- 推广到双边的窄基区二极管
- 令 WP′ 和 WN′ 分别是两侧准中性区的长度,且 WP′≪LP , WN′≪LN ,可以得到
I=qAni2[WN′NDDP+WP′NADN](ekTqVA−1)=I0(ekTqVA−1)
- 窄基区二极管的电荷控制模型:用少数载流子运输时间 τtr 代替 τp 或 τn 。
- 于是有
IDIFF=τPQP
分别计算 QP ,IP ,由于 Δpn 是线性的,所以在这里:
QP=qA∫xnWNΔpn(x)dx=qA 21Δ pn(xn)WN′
IP=AJP=−qADpdxdΔpn=qADpWN′Δpn(xn)
二者相除:
τtr,p=IpQP=2Dp(WN′)2
τtr,n=2DN(WP′)2
小信号导纳
- 小信号:一个正弦电压 vB 叠加在外加直流偏压上。
- 小信号导纳 Y=vgi 表征无源器件的交流响应。
- 小信号等效电路表示响应情况
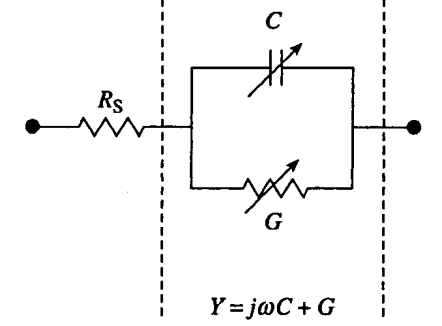
- pn 结二极管结区的响应包括电容和电导分量,导纳为 Y=G+jwC ( w 为交流信号的角频率)
- 前提:多数载流子需要快速流入/流出相关区域,也即器件随交流信号准静态变化(载流子可以对交流信号做出及时的响应,就如该信号是直流偏压的情况)。
反向偏置
反向偏置电容
- 电导很小, Y=jwC ;只与器件内的多数载流子振荡有关
- 小交流信号会导致耗尽层宽度在其稳态值附近进行小幅的摆动,因此有电容的效应。类似于平行板电容器,二极管的电容:
CJ=WKSεoA
- 反向偏置中 C=CJ ,由于 W 随反向偏压升高而增加,所以当反向偏压增大的时候 C 会降低。
- 我们会发现 W 和 VA 的关系随杂质分布而变化,这非常不方便,我们希望获得一个通用的表达式。由于这种变化主要来自杂质浓度分布的不同,因此我们用一个公式来表征上述分布 NB(x)=bxm…x>0 (其中 b>0 ,且 m 为常数)(这个式子表征了单边结的指数分布,也即一边重掺杂,一边轻掺杂的杂质浓度)
- m=0 对应非对称突变结
- m=1 对应单边线性缓变结
- m<0 称为超突变分布(超突变结)
- 代入后, m>−2 时耗尽层宽度关系式:
W=[qb(m+2)KSε0(Vbi−VA)]1/(m+2)
CJ=[qb(m + 2)KSε0(Vbi − VA)]1/(m+2)KSε0A
也可以用 CJ0 和 CJ 来描述上述电容关系
CJ0≡CJVA=0=[qb(m+2)KSε0Vbi]1/(m+2)KSε0A
CJ=(1 − VbiVA)1/(m+2)CJ0
- 有上述关系的 pn 二极管称为变容二极管。该二极管��的一个参数称为调制率 TR ,表征给定电压范围内二极管表现出的最大的电容比。
TR=C1(VA2)C1(VA1)≅(VA1VA2)1/(m+2)
(反偏时, VA≫Vbi ) m 越小, TR 越大。
- 计算相关参数:假设测试器件是非对称掺杂的突变结( m→0 与 b→NB ),采用上述电容公式并近似,有:
CJ21=qNBKSε0A22(Vbi − VA)
通过斜率和截距的关系,可以得到 NB 与 Vbi 等的数值。
反向偏置电导
- 假设二极管准静态地响应一个交流信号,那么交流电导就等于微分直流电导。
G0=dVAdI
- 理想二极管的式子 I=I0(eqVA/kT−1) 对 VA 求导。
G0=kTqI0eqVA/kT=kTq(I+ I0)
- 如果考虑复合-产生电流占主导地位(参见前面的修正)
G0=dVAd(−2τ0qAniW)=(m+2)(Vbi−VA)qAniW/2τ0
正向偏置
- 反向偏置导纳分析中引入结电容是多数载流子进入和离开稳态耗尽层引起的,此时少数载流子浓度的涨落对导纳的影响忽略不计。但在正向偏置中,交流信号引起的少数载流子电荷也会对结电容有贡献。
- 与多数载流子不同,当角频率接近少数载流子寿命的倒数时,少数载流子电荷的涨落很难与交流信号保持同步,而是异步的变化——增加测量电导,减小测量电容,并且依赖频率。
- 少数载流子在耗尽层边界的积累由扩散电流引起,导纳称为扩散导纳。
YD = GD + jωCD
计算过程
- 对 p+−n 结二极管:
- 要考虑少数载流子,就要利用少数载流子扩散方程
∂t∂Δpn(x,t)=Dp∂x2∂2Δpn(x,t)−τpΔpn(x,t)
- 交流信号带来的 Δpn(x,t) 的改变:
Δpn(x,t)=Δpn(x)+p~n(x,ω)ejωt
0=Dpdx2d2Δpn−τpΔpn
0=Dpdx2d2p~n−τp/(1+jωτp)p~n
Δpn(∞)=pn(∞)=0
直接把交流的电压代入前面推出的边界处的过剩载流子公式:
Δpn(x=xn)=Δpn(xn)+p~n(xn)=NDn12(eq(VA+vn)/kT−1)
已知直流形式与之前推出的相同:
Δpn(xn)=NDni2(eqVA/kT−1)
和上式相减,在采用无穷小时的近似:
p~n(xn)=NDni2eqVA/kT(eqva/kT−1)≅NDni2(kTqvaeqVA/kT)…va≪kT/q
- 利用边界条件,以及 τp→1+jwτpτp 的变化进行修正。得到:
idiff=G01+jωτpva
YD=υaidiff=G01+jωτp
- 如果是 n+−p 结的二极管: τp 换成 τn
- 分解实虚部
- 扩散电导(实部) GD=2G0(1+ω2τp2+1).1/2
- 扩散电容(虚部) CD=ω2G0(1+ω2τp2−1)1/2
- 低频( wτp�≪1 , 1+w2τp2≅1+w22τp2 )
GD→G0
CD→2G0τp
瞬态响应
- 关心 pn 结二极管在开关过程中达到的速度,在瞬态关断过程中,��速度受限最为显著。
- 前提:与二极管的最大正向压降 VON 相比,电源电压(无论正偏还是反偏)足够大。
关断特性
电路特性
- 什么是瞬态关断: t=0 之前在二极管两端加正向偏置电压并达到稳态, t=0 时刻开关打向反偏。
- 电流特性:开关转换后的瞬间,反向电流的大小与正向电流相当,在衰减到稳态值之前的时间内,基本保持常数。
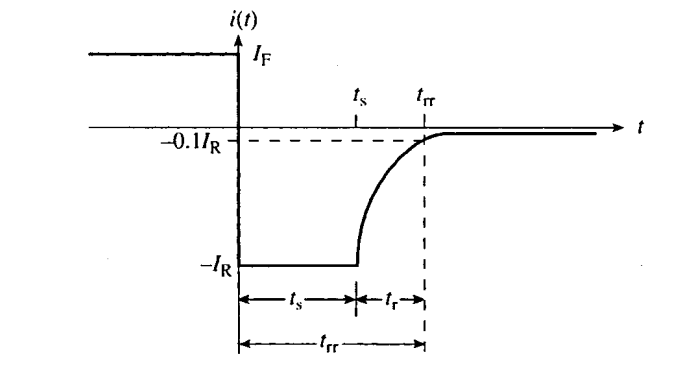
- 存贮延迟时间 ts :反向电流保持为常数的时间
- 反向恢复时间 trr :反向电流衰减到它最大数值 10% 所需的时间
- 恢复时间 tr :反向电流衰减的时间,前两者之差。
- 瞬时电压变化:

- 在存贮延迟时间仍保持正偏,在 t=ts 时等于 0
物理机制
- 二极管正向偏置时,使紧邻耗尽区的准中性区内��产生过剩少数载流子的积累;反偏时,紧邻耗尽区的少数载流子显著减少。过剩少数载流子需要一定的时间从准中性区移走,这时间就是存贮延迟时间。
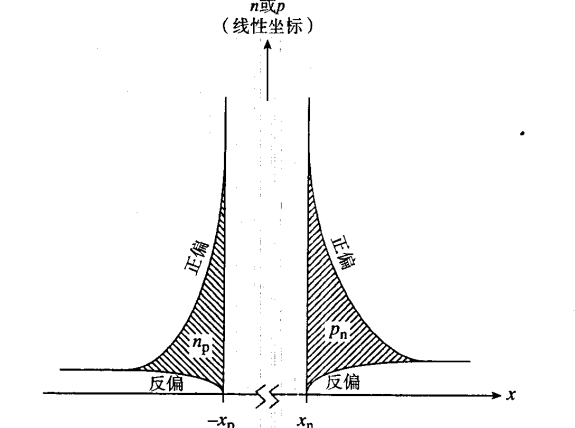
- 由电荷控制模型可知,由两种方法可以移走过剩少数载流子的电荷:
- 复合:如果是移走载流子的唯一方式,那么从开态到关态的时间与少数载流子的寿命相同。
- 净载流子漂移:流回结的另一边,非常快。此时二极管几乎等效为短路,最大反向电流由外电压 VR 与外电阻(保护电阻) RR 之比 IR 决定。
- 以上两种机理中没有一种可以以足够快的速度把电荷完全消除,因此会观察到延迟时间。
- 在 0∼ts 时,二极管如何保持正偏:对 p+−n 结二极管的过剩少数载流子而言,它与二极管两端的电压有如下的关系(这里我们用表示交流电压的 vA 代替 VA:
Δpn(xn)=NDni2(eqvA/kT−1)
从这个式子中我们可以观察到:当 vA 大于 0 时,紧邻耗尽层边界的区域中有过剩的少数载流子。实际上,是耗尽区边界与内部过剩载流子的存在才使结保持正偏。
考虑公式: i=AJP(xn)=−qADPdxdΔpnx=x0 ,可知:
dxdΔpnx=xn=−qADPi
这也是 pn(x,t)−x 图上 x=xn 处曲线的斜率。由于 0∼ts 时, i=−IR 为常数,所以对于所有 t>0 的曲线,在 x=xn 处的斜率必定相同。
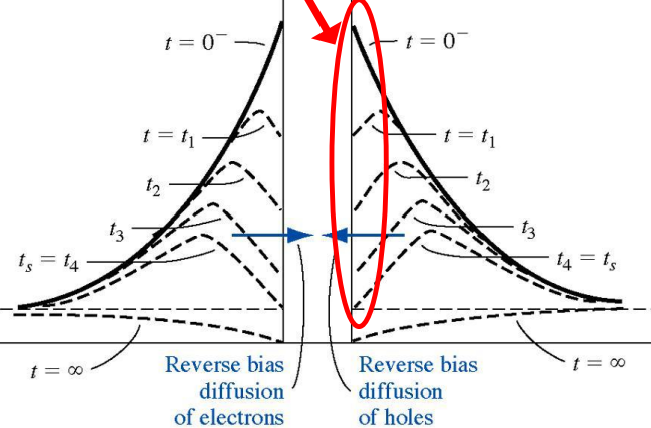
存贮延迟时间
- 推算存贮延迟时间 ts 的定量关系式:考虑 p+−n 二极管,使用电荷控制模型。(由于是单边结,相比 n 型一侧的空穴存贮电荷 QP 而言,存贮于 p 型一侧的电子电荷可以忽略;理想二极管,忽略耗尽区的R-G过程,故而 i=iDIFF )
- 0∼ts , i=−IR 为常数,代入电荷控制模型:
dtdQP= − (IR+τpQP)…0+⩽ t⩽ts
- 分离 QP 和 t ,从 t=0+ 到 t=ts 积分,得到
ts=−τpln(IR+τPQP)QP(0+)QP(ts)=τplnIR+τpQP(ts)IR+τpQP(0+)
QP(0+)=QP(0−)
关断时: dtdQP=0 且 i=IF 。代回前面列出的电荷控制模型方程,得到:
IF=τpQp(0−)=τpQp(0+)
同时假设 QP(ts) 近似为 0 。将这些条件代入前面得到的有关 ts 的式子中:
ts=τpln(1+IRIF)
- 从公式以及理解的角度,可以得到(当其他变量不变时):
- IF 变大,使得二极管的存贮�电荷增加,需要更长的时间来移走存贮电荷。
- IR 变大,意味着反向电流移走存贮电荷的速率增加,移走存贮电荷需要更短的时间。
- τP 减少,则少数载流子的复合速率增加,因此 ts 会减少。
- 阶跃恢复二极管 tr 不分很短,反向电流在达到 t=ts 之后快速地返回稳态值。
瞬态开启
- 什么是瞬态开启:二极管从反偏的关态切换到正偏的开态。可以通过电流脉冲或电压脉冲或两种脉冲的组合完成,这里只考虑电流脉冲。
电路特性
- 维持反偏电压的少子迅速注入耗尽区,多子迅速重分布,结电压迅速从反偏移动到 0V 。之后电压缓慢从 0V 上升到 VON 。
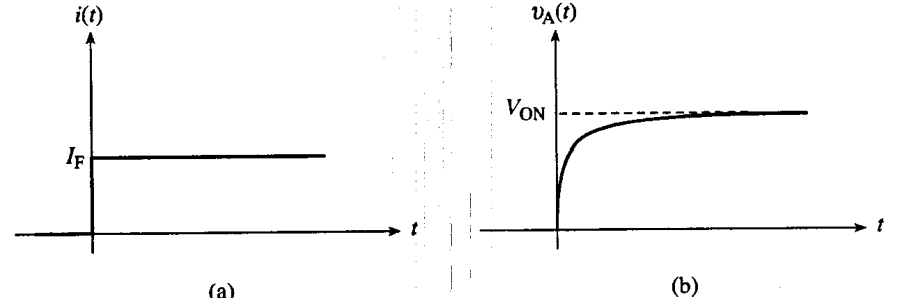
- 认为它是理想的 p+−n 突变结二极管,并采用电荷控制方法。显示预测的 n 型一侧空穴存贮电荷随时间的增加。
- 边界条件
- t=0 时 QP=0 。
- 瞬态开启过程中 i=IF
- 电荷控制方法
dtdQP = IF − τpQP
t=−τpln(IF−τpQP)0QP(t)=−τpln[1−IFτpQp(t)]
Qp(t)=IFτp(1−e−t/τp)
QP=IDIFFτp=I0τp(eqVA/kT−1)
由于是瞬态过程,用 vA 表示 QP(t) ,与上式联立,得到:
υA(t)=qkTln[1+I0IF(1−e−t/τp)]
- 结论
- QP(∞)=IFτP
- 瞬态开启的开始阶段有一个快速的上升,后期变得缓慢。
金属半导体接触
- 金属半导体从物理上和功能上,都与非对称的突变二极管 p+−n 或 n+−p 很相似。
MS分析
- 理想的MS接触
- 金属与半导体在原子尺度上紧密地接触,两者之间不存在任何夹层
- 金属和半导体之间不存在相互扩散或混合
- MS界面没有吸附的杂质或表面电荷。
- 能带图
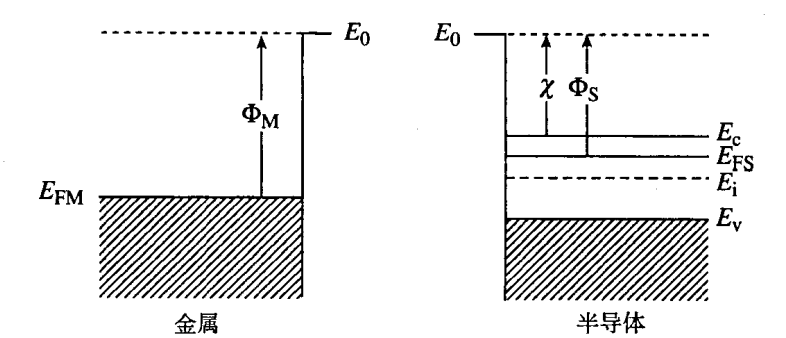
- E0 真空能级:电子完全脱离材料本身必须具有的最小能量
- Φ 功函数:真空能级与费米能级之间的能量差。
- ΦM 金属功函数,不变的基本参数,接触形成过程中保持不变
- ΦS 半导体功函数,公式:ΦS=χ+(Ec−EF)FB
- χ 电子亲和势, χ=(E0−Ec)∣surface ,对于一定的半导体材料是恒定的基本参数,在接触形成过程中保持不变
- (Ec−EF)FB 是在平带和零电场条件下 Ec 与 EF 之间的能量差。
- (Ec−EF)FB=2EG+EF−Ei
- EF−Ei=kTln(n/ni)=−kTln(p/ni)
- MS接触的过程
- 接触形成之��后的瞬间:金属和半导体的能带图以公共的 E0 参考能级为基准垂直地对齐,并在界面处对接。此时,由于费米能级不相等,故而MS接触明显处于非平衡态。
- 之后,载流子会根据半导体的类型与势垒的大小流动,达到平衡态。
n型半导体
ΦM>ΦS 的情况
- 刚接触时:
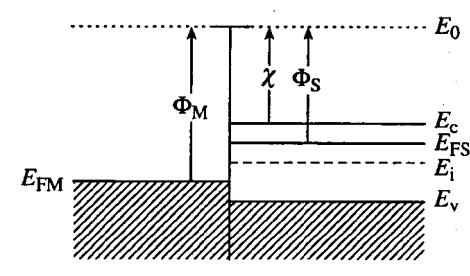
- 之后,电子从半导体向金属内转移(因为 n 型半导体的费米能级高于金属的 EFM ),而电子损失导致电子势垒的增加,阻止电子从半导体向金属内转移,直到电子的转移和势垒的阻止互相抵消,此时 EF 在整个结构中都一样。
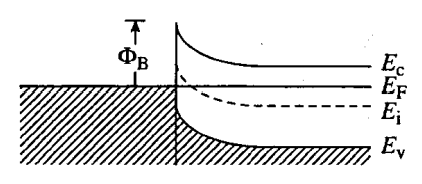
- 注意在边界处的能带不发生变化,但在无限远处 EF 与金属的 EFM 齐平。其中 ΦB=ΦM−χ 是在金属中具有 E=EF 能量的电子遇到的表面势垒。
- 肖特基势垒实际上既阻止电子从金属到半导体,也阻止电子从半导体到金属,只不过后者更容易一些,而且会受到外加电压的影响。
添加偏压 VA>0
- EFM<EFS ,对半导体中的电子而言势垒降低,有电流从半导体流向金属。 VA 增加,正向偏置电流快速上升,可以越过表面势垒的电子数量呈指数增加。
- 示意图:
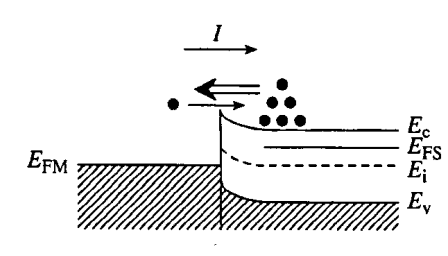
添加偏压 VA<0
- EFM>EFS ,阻止电子从半导体向金属的流动;同时金属中只有很少的电子可以越过 ΦB 势垒,反向偏置电流相对较小。
- 示意图:
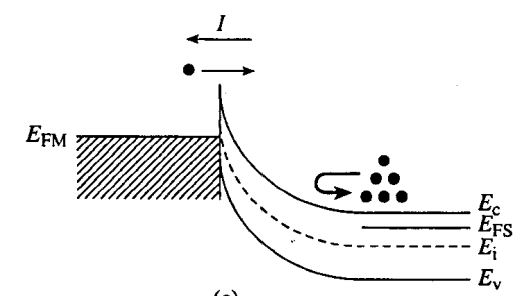
- 类似于 pn 结二极管,具有整流特性or整流接触。
- 金属与 p 型半导体接触,其中 ΦM<ΦS 的情况与这种情况类似,示意图:
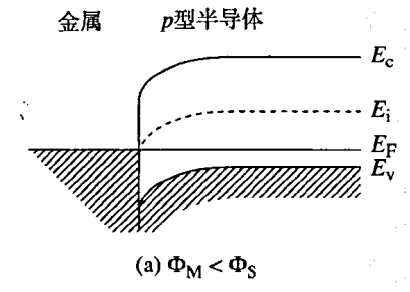
ΦM<ΦS 的情况
- 刚接触时:
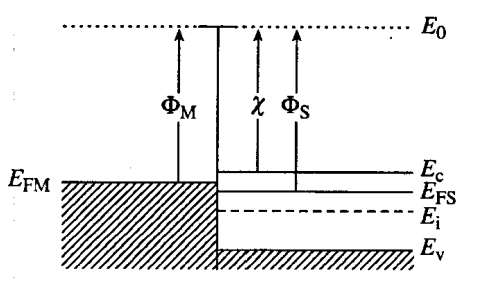
- 之后,由于 EFM 和 EFS 之间的差距比较小,所以电子在半导体和金属之间自由流动,达到平衡状态。
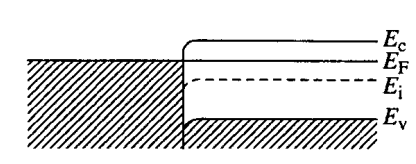
- 这里的 ΦB 不是特别大。
添加偏压 VA>0
- 没有任何势垒,很小的电压就会造成很大的正向偏置电流。
添加偏压 VA<0
- 从金属到半导体有一个很小的势垒
- 反偏超过零点几个伏特时,势垒就变为 0
- 较小的反偏电压下就有比较大的反偏电流,而且反偏电流不会饱和。
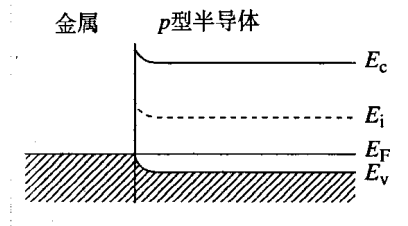
- 非整流型的/欧姆型的接触。
- 金属与 p 型半导体接触时,其中 ΦM>ΦS 的情况与这种情况类似,示意图:
肖特基二极管
静电特性
- 回顾一下内建电压的概念:在分析理想 pn 结的时候,内建电压来源于势垒,也就是当两个半导体拼在一起的时候,它们费米能级的差值再除以 q 。ok,我们把这个思路迁移到整流MS二极管上:

- ΦBn 是肖特基势垒。
- 从这个图中我们把金属和半导体拼在一起,明显看到 EFM 和 EFS 之间的差值是 ΦM−ΦS 。但 ΦS 实际上是算出来的,它等于 χ+(EC−EFS)FB ,我们把这个式子代入,并且用 ΦB 代替 ΦM−χ ,所以就可以得到:
Vbi=q1[ΦB−(Ec−EF)FB]
- 考虑载流子堆积的情况。对 n 型MS接触(整流),由于半导体中的电子流向金属,半导体中会出现一个耗尽区,宽度为 xn ,耗尽区中具有施主离子产生的净正电荷。不过,在金属一侧,不会出现负的受主电荷了。所以,MS接触中,正电荷以如下方式进行堆积
ρ≅{qND0…0⩽x⩽W…x>W
在交界处,负电荷以冲激函数的形式存在,半导体一侧的空间正电荷把金属中的空间负电荷吸引到结区的边缘,且金属中的自由负电荷非常多,因此形成了冲激函数。
dxdE=Ksε0ρ≅Ksε0qND… 0⩽x⩽W
得到:
E(x)=−KSε0qND(W−x)...0⩽x⩽W
V(x)=−2KSε0qND(W−x)2…0⩽x⩽W
- 等效于 pn 结分析中的结果,只是电势不同(在这里,我们为了分析方便,将电势参考点选在半导体表面,方便对半导体进行分析),因此在 x=0 处,电势为 −Vbi (此处刚好是金属的电势,但我们设半导体的电势为 0 点,同时要考虑电子电荷为 −q 对能带的影响),加入并考虑外加电场 VA ,可以假设 x=0 处 V=−(Vbi−VA) 。
- 代入上述 V 可以解出耗尽区宽度
W=[qND2KSε0(Vbi − VA)]1/2
I-V特性
- 对MS二极管( n 型)来说,正偏时电流主要来源于半导体进入金属电子注入(势垒非常低),耗尽层中的复合电流与空穴扩散可以忽略(我很好奇一个金属哪来的空穴),示意图
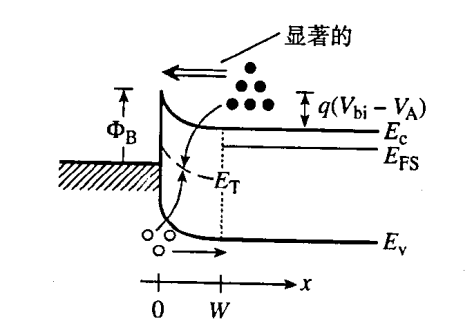
- 反偏时电流主要来自金属流向半导体的电子流,反偏空穴扩散电流与耗尽区的载流子相关的R-G电流一般可以忽略。
- MS二极管称为“多数载流子器件”
- 正偏时,电子越过势垒进行注入,可看做热电子发射电流
KEx=21 mn⋆υx2≥q(Vbi − VA)
- 可以通过解出电子速度 vx 从而得到与电子相关的电流
IS∙→M,νx=−qAυxn(υx)
(此处省略一个 n(vx) 的推导式子,感觉贴了也没啥用,想看看书P352页罢,半导体器件基础那本(雾),总而言之,可以简化得到:
IS∙→M=AA∗T2e−ΦB/kTeqVA/kT
A∗≡(m0∗mn∗��)A
理查森常数:
A≡h34πqm0k2=120amps/(cm2⋅K2)
电子从金属到半导体,穿过界面时遇到的势垒高度 ΦB 始终不变,并且基本不受到外加电压的影响,于是有:
IM∙→S(VA)=IM∙→S(VA=0)
且,平衡时无电流,所以可以得出:
IM∙→S(VA=0)=−IS∙→M(VA=0)=−AA∗T2e−ΦB/kT
I=IS∙→M+IM∙→S=IS∙→M+IM∙→S(VA=0)
I=Is(eqVA/kT−1)
Is=AA∗T2e−ΦB/kT
交流响应
- 交流小信号加在直流反偏电压上,MS界面处 δ 函数电荷发生波动,多数载流子从半导体中快速地移进移出,耗尽区宽度也发生波动。示意图
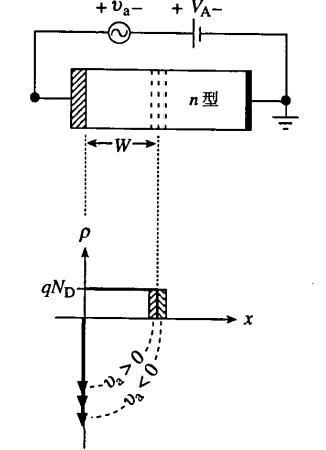
- 电容类似于突变结且一边重掺杂的半导体的电容,有:
C21=qNDKSε0A22(Vbi−VA)
如果 Vbi 和 ND 已知,即可算出 ΦBn
qVbi=ΦBn−(Ec−EF)FB=ΦBn−kTln(NDNc)
欧姆接触
- 由于费米能级钉扎效应的存在,很难满足欧姆接触的条件。
- 实际上,要达到欧姆接触,需要高掺杂率的半导体,这样载流子可以隧穿过势垒。
- 比接触电阻率(每单位面积的接触电阻)
R=Aρc
就实际的欧姆接触而言:
ρc∝eHΦB/ND


 以 为周期进行平移,得到
以 为周期进行平移,得到



 注意这里的能级表现为一组非连续的线,因为束缚电子和施主之间的距离是局域化的,也就是图中 的范围
注意这里的能级表现为一组非连续的线,因为束缚电子和施主之间的距离是局域化的,也就是图中 的范围








 相关公式:
相关公式:
 复合:首先一种载流子漂移进入R-G中心附近,被相关势阱捕获,失去能量;之后出现另一种载流子,二者互相吸引,失去能量,在中心内与电子一同湮灭。也有可能,电子失去能量后,在价带与空穴一起湮灭。产生过程也类似,热能作为中间媒介,在R-G中心产生载流子。
复合:首先一种载流子漂移进入R-G中心附近,被相关势阱捕获,失去能量;之后出现另一种载流子,二者互相吸引,失去能量,在中心内与电子一同湮灭。也有可能,电子失去能量后,在价带与空穴一起湮灭。产生过程也类似,热能作为中间媒介,在R-G中心产生载流子。
































