大学物理电学知识汇总

真空中的静电场

• 无限长均匀带电直线，电荷线密度为$\lambda$，其电场强度方向垂直于带电直线的矢径。$E(r)=\frac{\lambda}{2\pi \epsilon_{0}r^{2}}\vec{r}$
• 无限大均匀带电平面： $E=\frac{\sigma}{2\epsilon_{0}}$
• 带电圆板在距离中心$x$处的电场强度为：

$$E=\frac{\sigma}{2\epsilon_{0}}\left( 1-\frac{x}{\sqrt{ x^{2}+R^{2} }} \right)$$

• 高斯定理：

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc \vec{E}·d\vec{s}=\frac{1}{\epsilon_{0}} \sum_{i=1}^nq_{i}$$

注意：高斯定理也有其变式（大学物理教程（下）12-8，第二问）：

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc \Delta\vec{E}·d\vec{s}=\frac{1}{\epsilon_{0}} \sum_{i=1}^n\Delta q_{i}$$

高斯定理的微分形式：

$$\nabla \cdot \vec{E}=\frac{\rho}{\epsilon_{0}}$$

• 环路定理：

$$\oint_{l}\vec{E}·d\vec{l}=0$$

• 环路定理的两个应用：
  • 电介质（切向）的边值条件
  • 算一些特殊电场线中的电场关系
• 电势：

$$V_{a}=\int^b_{a}\vec{E} \cdot\, d \vec{l}$$

（注意：$b$点为电势的零点）（计算电势要注意正负号）

$$V_{a}-V_{b}=\int _{a}^b E\, dl$$

（这个是反的！）

• 电势与电场强度的关系：

$$\vec{E}=-\nabla V$$

极坐标系中：

$$\nabla =\frac{\partial}{\partial r}\vec{e_{r}}+\frac{1}{r} \frac{\partial}{\partial \theta} \vec{e_{\theta}}$$

最高/最低电势满足条件：

$$\frac{dU}{dx}=0 或 E_{x}=0$$

其中：电势必须是连续的，而场强可以是不连续的（指图像）

---

电偶极子相关

• 电偶极矩：

$$\vec{p}=q \vec{l}$$

注意：$\vec{l}$是正电荷相对于负电荷的位置矢量

• 电势为：

$$V(r,\theta)=\frac{\vec{p}\cdot\vec{r}}{4\pi \epsilon_{0} r^3}$$

注意：$\vec{r}$是相对于电偶极子中心的位置矢量

• 电场强度为：

$$\vec{E}=\frac{1}{4\pi\epsilon_{0}r^3}\left[ -\vec{p}+\frac{3(\vec{r}·\vec{p})\vec{r}}{r^2} \right]$$

轴线上的电场强度：

$$\vec{E}=\frac{\vec{p}}{2\pi\epsilon_{0}r^3}$$

• 力矩：

$$\vec{M}=\vec{p} \times \vec{E}$$

力矩做功

$$W=M\cdot\theta$$

• 电势能：

$$W=-\vec{p}\cdot \vec{E}$$

• 非匀强电场$E$中，电偶极子受到电场的作用力：

$$\vec{F}=\nabla (\vec{E}\cdot \vec{p})=-\nabla W$$

---

• 半无限长直导线在端点所在的垂直于导线的平面的场强可以等效为一个四分之一圆弧在这一点的场强。
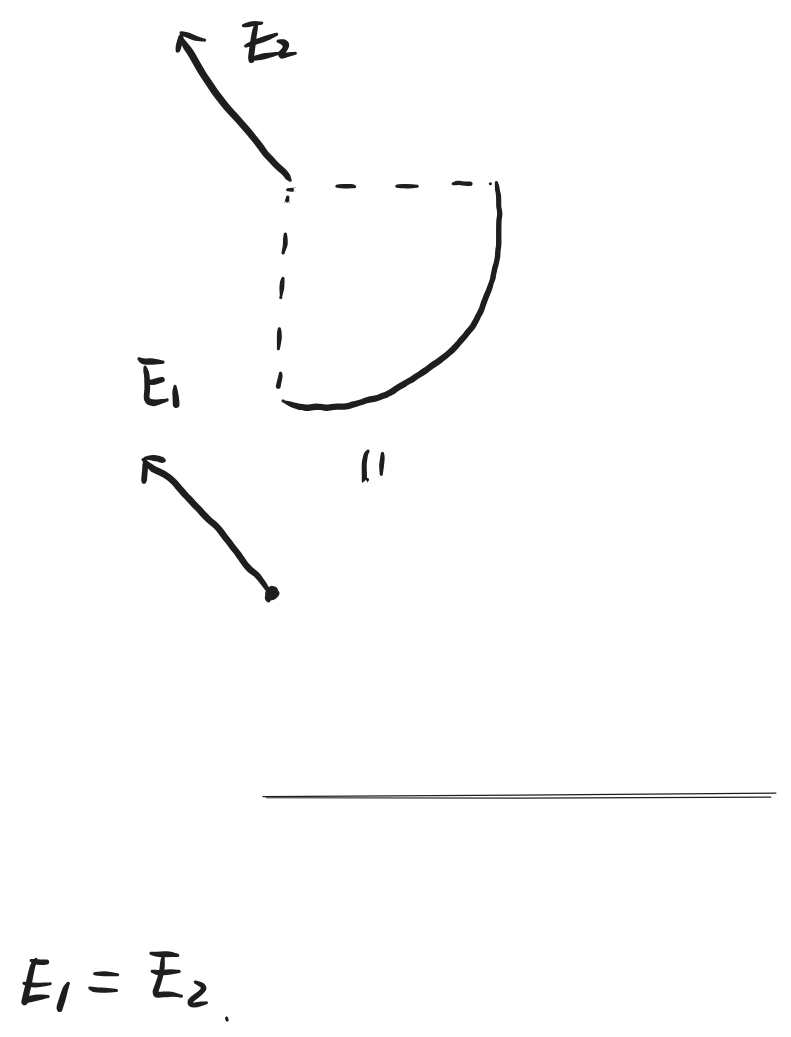
• 等效（取微元）时，注意：要么可以用微积分表示其规律，要么相对位置一致，可以叠加
• 计算电偶极子相关时，注意合并相同的量

静电场与物质的相互作用

导体

• 导体表面电荷分布：

$$\vec{E}=\frac{\sigma}{\epsilon_{0}}\vec{e_{n}}$$

（$E$实际上是由导体表面上所有电荷分布，以及可能存在的外加电场共同决定的） （注意与无限大平面之间的区别）

• 平行板电容器：外侧空间电场强度为$0$，内侧空间电场强度为（等效为了四个无限大平板）：

$$E=\frac{\sigma}{\epsilon_{0}}$$

---

• 条件转换：导体接地=导体为零电势的等势体（带电量不一定为$0$哦，12-11（5））
• 均匀带电球面：球面外的电场分布与所有电荷集中在球面中心的点电荷的电场相同；球面内部的电场强度恒为0，所以球面里的电荷不受力！！！
• 平行板电容器为何板外电场为$0$？因为二板相距比较近，外侧可以抵消
• 如果导体平板接地，那么接地侧电场恒为$0$。原因是考虑到无穷远处电势为$0$，导体电势也为$0$，故两者连线上电场处处为$0$。
• 导体/电介质缺掉一块，求剩下的部分在这一点的电场/对这一块电荷的力：设这一小块的电场为$E_{1}$，大块对小块的电场为$E_{2}$，根据被挖去这块两边的电场关系求出$E_{1}$与$E_{2}$（这里涉及到电场强度的叠加）
• 关于导体球壳的终终极总结：如果$A$球在$B$球内：$A$球接地，约束条件为：$A$球内电势为$0$；$B$球接地，约束条件为：球外电场为$0$。
• 相距很远的两个球形导体：互不影响（指电场互不影响）；俩导体用导线连起来，可以看作电容串联

电介质(一定注意是否均匀)

• 极化强度矢量的定义：单位体积内电矩的多少，单位$\frac{C}{m^2}$
• 均匀极化，极化强度为$P$的电介质球，在球内产生匀强电场的值为$\frac{\vec{P}}{ 3 \epsilon_{0}}$
• 电介质内电场强度：

$$\vec{E}=\vec{E_{0}}+\vec{E'}$$

• 对各向同性的电介质,极化强度与电场强度的关系：

$$\vec{P}=\chi_{e}\epsilon_{0}\vec{E}$$

• 极化电荷面密度与极化强度的关系（均匀极化）：

$$\sigma'=\vec{P}\cdot \vec{e_{n}}$$

• 极化电荷体密度与极化强度的关系（不均匀极化）：（一定要注意负号）

$$\rho'=-\nabla \cdot \vec{P}$$

• 介质中的环流定理：

$$\oint_{l}\vec{E}\cdot d \vec{l}=0$$

• 电位移矢量的定义：

$$\epsilon_{0}\vec{E}+\vec{P}=\vec{D}$$

• 介质中的高斯定理： 注意：$q_{0}$是自由电荷。

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc_{s}(\epsilon_{0}\vec{E}+\vec{P})\cdot d \vec{S}=\sum_{S内}q_{0}=\int\kern{-8pt}\int \kern{-23mu} \bigcirc_{s}\vec{D}\cdot d \vec{S}$$

• 对各向同性介质，外加电场不太强时，介质对电场的响应为线性的电介质（对永久极化的驻极体不成立）（$E$是电介质外加电场）：

$$\vec{D}=\epsilon_{0}(1+\chi_{e})\vec{E}=\epsilon_{0}\epsilon_{r}\vec{E}$$

其中：$\epsilon_{r}=(1+\chi_{e})$ 于是有$\vec{D}=\epsilon \vec{E}$ 注意：$\epsilon$是介电常数，$\epsilon_{r}$是相对介电常数，$\epsilon_{0}$是真空介电常数

---

应用：静电场的边值关系

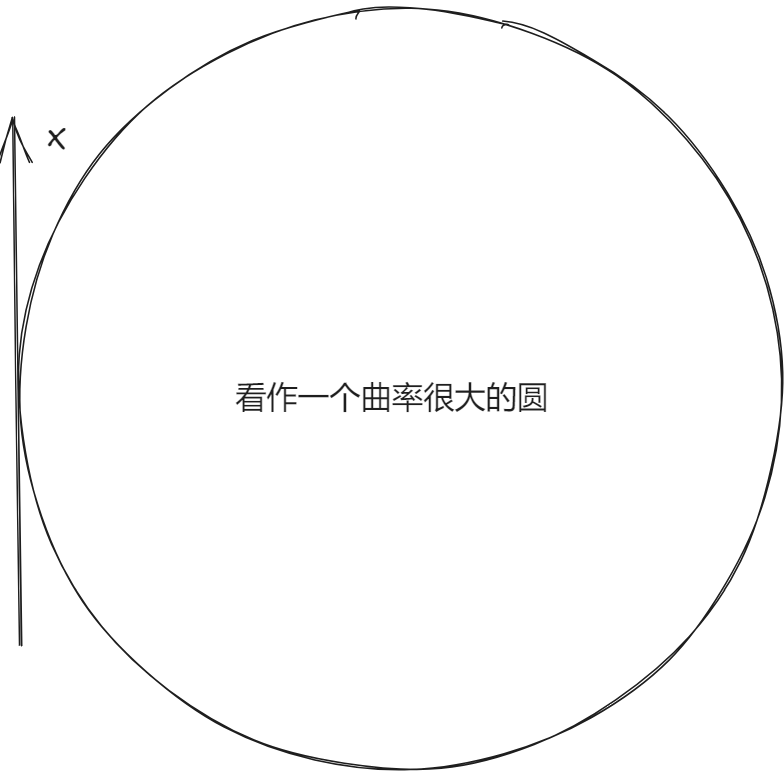
• 两介质界面中无自由电荷存在时，两介质中电场的法向分量：

$$\epsilon_{1}E_{1}=\epsilon_{2}E_{2}$$

• 切向分量：

$$E_{1}=E_{2}$$

电容

• 电容的定义式：（$V$是电势）

$$C=\frac{q}{V}$$

• 电容器的电容：（$\Delta V$是电势差）

$$C=\frac{q}{\Delta V}$$

• 平行板电容器的电容：

$$C=\frac{\epsilon_{0}S}{d}$$

• 球形电容器的电容（半径分别为$R_{A}$与$R_{B}$，里面充满了介电常数为$\epsilon$的电介质）：

$$C=\frac{q}{\Delta V}=4\pi\epsilon \frac{R_{A}R_{B}}{R_{B}-R_{A}}$$

• 圆筒形电容器的电容：

$$C=\frac{2\pi l\epsilon_{0}}{\ln \frac{R_{2}}{R_{1}}}$$

• 电容器的连接：判断串并联的方法：看每个电容器两端的电势差和总电势差之间的关系。 串联：

$$\frac{1}{C}=\sum_{i} {\frac{1}{C_{i}}}$$

并联：

$$C=\sum_{i}C_{i}$$

静电场的能量（系统的电势能）

• 点电荷的静电相互作用能：

$$W_{e}=\frac{1}{2}\sum^n_{i}q_{i}V_{i}$$

• 连续分布带电体的静电相互作用能：

$$W_{e}=\frac{1}{2}\int V \, dq$$

• 电容器的静电能

$$W_{e}=\frac{1}{2}{\frac{Q^2}{C}}$$

• 电容器取出电介质时的能量 $W_{e}=W_{f}+U\Delta Q$
• 单位体积中静电场的能量/系统的静电能（能量密度）

$$w_{e}=\frac{1}{2}\epsilon E^{2}$$

其中$\epsilon$是介电常数。注意$E$的平方。

• 对各向同性的均匀介质

$$w_{e}=\frac{1}{2}\vec{D}\cdot\vec{E}$$

• 因此，另一种静电场能量的算法：

$$W_{e}=\iiint_{\Omega}w_{e}dV=\frac{1}{2}\iiint_{\Omega }\vec{D}\cdot \vec{E} dV=\frac{1}{2}\iiint_{\Omega}\epsilon E^2dV$$

---

电像法

• 无限大平面：对对面的电荷做镜像
• 导体球（接地）的等效：
  • $Q'=-\frac{R}{a}Q$
  • $b=\frac{R^2}{a}$

其中a是电荷距球心的距离，b是像电荷距球心的距离，R是导体球的半径。 $\mid Q'\mid<Q$，所以$Q$发出的电力线只有一部分收敛于导体球，剩下的伸展至无穷。 若不接地，则导体球的带电情况为接地的导体球+一个均匀带相反电量的导体球。

需要注意的地方

• 积分时，有时使用三角函数会更简单，要注意角度是否统一
• 注意球面与球壳的区别/电容器：注意球形与圆柱形电容器的区别
• 多个带电体相互影响：电势叠加
• 计算合电场：可以先建系，分别计算系上两个坐标方向的电场。
• 接地的限制条件是电势为$0$
• 设$q$或$\sigma$的时候，要考虑它实际上与什么量相关，相关的量的表达式中是否有变量
• $\sigma$是面密度，$\rho$是体密度
• 不要忘记一些负号，譬如求$\nabla$之后的
• 电像法注意负号
• 极化强度（$\vec{P}$）和电位移矢量（$\vec{D}$）不是一个东西

数学基础

• 球面积分（注意多出的$\sin\theta$）

$$ds=r^{2}\sin \theta d\theta d\psi$$

参见：球面积分 - 知乎 (zhihu.com)

• 球体积分

$$dV=r^2\sin \theta d\theta d\psi dr$$

• 沃利斯公式

电流

目的： 将电流和电荷以及电场联系起来

• 电源的非静电力强度：($q$为载流子带电量)

$$E_{k}=\frac{F_{k}}{q}$$

• 电源的电动势：（单位正电荷从负极移到正极，也可以单位正电荷对闭合回路的积分）

$$\epsilon=\int_{-}^+ \vec{E_{k}} \cdot d\vec{l}$$

• 导体内的电流强度$I$：

$$I=\frac{dq}{dt}$$

• 描述电流空间分布性质的$\vec{j}=\vec{j}(x,y,z)$：（方向平行于相应空间稳恒电场的方向）（$\vec{e_{n}}$垂直于电场方向的截面的法线方向）

$$\vec{j}=\frac{dI}{dS_{\bot}}\vec{e_{n}}$$

• 导体内部通过任意面元$d\vec{S}$的电流强度为：

$$dI=\vec{j}\cdot d\vec{S}$$

通过导体中任意曲面$S$的电流强度$I$：

$$I=\iint_{S} \vec{j}\cdot d\vec{S}$$

（电流强度的正负与通过曲面$S$的法线方向的选择有关）

• 金属导体中的电流密度：

$$\vec{j}=nq \vec{v}\_{d}=n\_{+}q\_{+} \vec{u}\_{+}+n\_{-}q\_{-}\vec{u}\_{-}$$

导体中每个载流子电量为$q$，数密度为$n$，平均漂移速度为$v_{d}$；理论上，$q_{+}$或者$q_{-}$应该是有正有负的。但如果用离子的迁移率$\frac{u}{E}$来表示，迁移量这个值本身就代表了其正负，因此就不用再代入正负了。（课后题13-4）

• 电子平均漂移速度（由电场算出加速度后算平均速度后出）：

$$v_{d}=-\frac{\mid e\mid E}{2m}\tau$$

代入上式之后：

$$\vec{j}=\frac{ne^2\tau}{2m} \vec{E}=\gamma \vec{E}$$

$\gamma$为导体的电导率。

• 电流元和电荷元的转换：

$$Id \vec{l}=S(nqv_{d})d \vec{l}=dq \vec{v}_{d}$$

磁场

• 磁作用力与磁场（发现过程及定义）：

$$\vec{F}=qv\times \vec{B}$$

$B$是磁感应强度，单位是特斯拉，$1T=1N \cdot s / (C\cdot m)$ 高斯：$1G=1 \times 10^{-4}T$

电生磁及其应用

• 毕奥-萨伐尔定律（实验定律）：

$$d \vec{B}=\frac{\mu_{0}}{4\pi} \frac{I d \vec{l} \times \vec{r}}{r^3}$$

$\vec{r}$是目标点相对于电流元的位矢 使用该公式的时候注意电流元的选取，同时注意考虑图中出现的所有导线对所求点的磁感应强度的影响（和所求点在同一直线上的导线对所求点的磁感应强度没有影响）（习题13-6）

电流元的磁场

• 直电流对距离其为$r$的空间点的磁感应强度大小：

$$B=\frac{\mu_{0}I}{2\pi r}$$

（方向：右手螺旋，大拇指指向电流方向）

• 圆电流在其轴线上一点产生的磁感应强度：

$$B=\frac{\mu_{0} I R^2}{2(R^2+z^2)^{3/2}}$$

$z=0$时，$B_{0}=\frac{\mu_{0}I}{2R}$，若是一段圆弧：$B=\frac{\mu_{0}I}{4\pi R}\theta$，$\theta$是圆弧的圆心角。 $z\gg R$时，$B_{P}=\frac{\mu_{0}IR^2}{2z^3}$，这时，令$\vec{m}=IS \vec{e_{n}}$，原式可以写成$B_{P}=\frac{\mu_{0}}{2\pi} \frac{\vec{m}}{z^3}$

• 载流圆线圈（任何平面载流线圈）可以称为磁偶极子。$\vec{m}$为对应的磁矩。磁矩的定义：

$$\vec{m}=NIS \vec{e_{n}}$$

• 无限长直流载流螺线管轴线上任意点的磁感应强度（$n$螺线管轴线方向上单位长度线圈数量）：

$$B=\mu_{0}nI$$

• 半无限长螺线管端面（13-14）中心处磁感应强度大小：

$$B=\frac{1}{2}\mu_{0}nI$$

运动带电粒子的磁场

• 利用$Id\vec{l}=S(nqv \_{d})d\vec{l}=dNq \vec{v}\_{d}$（$dN$是电流元对应导体部分的载流子数目）。

  代入毕奥-萨伐尔定律：

$$B=\frac{\mu_{0}}{4 \pi} \frac{q \vec{v} \times \vec{r}}{r^3}$$

• 磁场与电场的关系： 利用：

$$\vec{E}=\frac{q}{4\pi\epsilon_{0}} \frac{\vec{r}}{r^3}$$

和上式得出（课本13-17）。

磁场的性质

• 磁通量（单位：韦伯$Wb$，$T \cdot m^{2}$：

$$\Phi _{m}=\iint\_{S}\vec{B} \cdot d \vec{S}$$

• 高斯定理：

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc \vec{B} \cdot d \vec{S}=0$$

• 环路定理：

$$\sum_{i}(\oint_{l} \vec{B_{i}} \cdot d \vec{l})=\mu_{0} \sum I$$

注意：$\vec{B}$是整个空间所有电流分布产生的磁场。 从负无限大到正无限大可以看作一个回路，对其应用环路定理可以得到$\int _{L} \vec{B} \cdot d \vec{l}$的值。

求磁场具体的值之前首先要确定磁场的方向。

• 利用高斯定理推知无限长螺线管内部的磁场的思路：
  • 设三个方向的磁场
  • 利用高斯定理/环路定理将三个方向排除至一个方向
  • 利用环路定理推匀强磁场
  • 利用高斯定理推螺线管外部磁场为0
  • 利用环路定理求解
• 无限大均匀载流平面的磁场（与平面平行，具体方向看平面内电流的方向）（注意是匀强磁场哦）：

$$B(z)=\frac{\mu_{0}\alpha}{2}$$

其中$\alpha$是单位宽度内的电流强度：

$$\alpha=\frac{\Delta I}{\Delta l}$$

• 磁场的磁感应强度可以相加：

$$\vec{B}=\vec{B_{1}}+ \vec{B_{2}}$$

注意：当磁场的磁感应强度的大小和方向确定后，就只能相加而不能相减（13-15）。

磁场对载流导体/带电粒子的作用

• 利用电流元和电荷元的转换以及磁感应强度的定义式可知：

$$d \vec{F}=I d \vec{l}\times \vec{B}=dq \vec{v}_{d} \times \vec{B}$$

载流导体

• 载流导体$L$受到的磁场作用力（注意这里是叉乘）：

$$\vec{F}=\int d \vec{F}= \int_{L} I d \vec{l} \times \vec{B}$$

• 磁场中平面载流线圈受力矩与磁矩之间的关系：

$$\vec{M}=\vec{m} \times \vec{B}$$

$\phi=\pi$，不稳定平衡位置 $\phi=0$，稳定平衡位置

• 安倍力做功： 当电流保持不变的时候

$$dA=I d \Phi_{m}$$

计算相关磁通量时要注意方向。 当磁场中的分子或者原子以磁矩的形式存在于磁场中时：

$$dA=d(\vec{m} \cdot \vec{B})$$

相应分子在磁场中的能量为：

$$U=- \vec{m} \cdot \vec{B}$$

磁矩做功：

$$-W=U_{f}-U_{i}$$

受磁场的作用力$F$

$$\vec{F}=\nabla (\vec{m} \cdot \vec{B})$$

带电粒子

• 洛伦兹力：

$$\vec{F}=q \vec{v} \times \vec{B}$$

• 轨道半径：

$$R=\frac{mv(\sin \theta)}{qB}$$

• 运动周期：

$$T= \frac{2\pi m}{qB}$$

• 螺距：

$$h=\frac{2\pi m v \cos \theta}{qB}$$

在这里recall一些高中知识：粒子在电磁场中运动时，要将其洛伦兹力分解为一个可以抵消电场力的力，将运动简化为匀速直线运动+圆周运动。 粒子有从强磁场区域向弱磁场区域运动的趋势。

霍尔效应：对上述两者的应用

![霍尔效应]（/img/wldx/霍尔效应.png) 相关公式：

$$I=n\mid e\mid v bd$$ $$E=vB$$

霍尔电压：

$$\Delta U_{H}=\frac{1}{n\mid e\mid} \frac{BI}{d}$$

霍尔系数：

$$R_{H}=\frac{1}{n\mid e\mid}$$

磁场与物质的相互作用

• 稳恒电流激发磁场与介质中磁场的关系

$$\vec{B}=\mu_{r}\vec{B}_{0}$$

• 电子的磁矩

轨道磁矩：

用$m=IS$的关系算出

$$\vec{\mu}_{l}=-\frac{\mid e\mid}{2m}\vec{L}$$

$\vec{L}$是其角动量。

自旋磁矩：

$$\vec{\mu}_{s}=-\frac{\mid e \mid}{m}\vec{S}$$

$\vec{S}$为其自旋角动量。

电子磁矩：

$$\vec{\mu}\_{e} = \vec{\mu}\_{l} +\vec{\mu}\_{s}$$

当电子在磁场中运动，且轨道角动量与磁场方向不平行时，将绕磁场方向进动，从而带来一个附加轨道磁矩，削弱介质中的磁场。

• 分子磁矩

$$\vec{\mu}\_{m}=\sum\_{i}\vec{\mu}\_{ei}$$

抗磁质：分子磁矩为$0$的介质（附加磁场导致抗磁,$\vec{M}$的方向与外磁场方向相反） 顺磁质：分子磁矩不为$0$的介质（磁矩转向导致顺磁，$\vec{M}$的方向与外磁场方向一致）

• 无论是抗磁质物质还是顺磁质物质，无外加磁场时，磁介质分子磁矩的矢量和为$0$。加入磁场，介质磁化程度随磁场大小增强/减弱。
  • 均匀磁化的磁介质：表面存在分子电流，内部不存在。非均匀磁化的磁介质：内部和表面均存在分子电流。
  • 磁化强度矢量：

$$\vec{M}=\lim_{ \Delta V \to 0 } \frac{\sum_{\Delta V}\vec{\mu}_{mi} }{\Delta V}$$

磁化强度的单位是$A\cdot m^{-1}$

• 磁化强度与磁化电流的分布：

$$\vec{\alpha'}=\vec{M}\times \vec{e}_{n}$$

• 利用介质斜柱形体元的磁矩可以看作一个磁偶极子，以及公式$\alpha'=\frac{dI'}{dl}$（其中$l$的方向与$I$的方向垂直，注意线电流的含义，例14-1）得出。其中 $\vec{e}_{n}$ 为介质体元表面的方向。

  • 外磁场中介质中任一点

$$\vec{B}=\vec{B}_{0}+\vec{B}'$$

• 介质中磁场的高斯定理：

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc \vec{B} \cdot d \vec{S}=0$$

• 介质中磁场的安倍环路定理

$$\oint_{l}\vec{H} \cdot d \vec{l}=\sum I$$

当$H$的值有所不同时：（14-13）

$$\oint_{l}\vec{H} \cdot d \vec{l}=\sum H_{i}l_{i}$$

其中：

$$\frac{\vec{B}}{\mu_{0}}-\vec{M}=\vec{H}$$

$\vec{H}$称为磁场强度，受传导电流和磁化电流的影响，单位同磁化强度，没有物理意义。$I$是闭合曲线$l$所围的传导电流。如果不存在磁介质，则$\vec{M}=0$。

• 磁化强度$\vec{M}$和磁场强度$\vec{H}$的关系

$$\vec{M}=\chi_{m} \vec{H}$$

$\chi_{m}$为介质的磁化率。顺磁质大于$0$，抗磁质小于$0$，影响磁化强度和磁场强度的方向。

• 磁感应强度$B$与磁场强度的关系$H$

$$\vec{B}=\mu_{0}(1+\chi_{m}) \vec{H}=\mu_{0}\mu_{r} \vec{H}$$

$\mu \_r$ 为相对磁导率， $\mu=\mu\_{0}\mu\_{r}$ 是介质的磁导率。在解题时需要注意使用介质相应的磁导率解题。

• 螺绕环的磁场强度

$$H=\frac{NI}{2\pi r}=nI$$

$n=\frac{N}{2\pi r}$，为螺绕环单位长度的匝数。

• 介质交界面磁场的关系

$$B_{1n}=B_{2n}$$

用高斯定理推出。

$$H_{1t}=H_{2t}$$

用环路定理推出。

• 磁滞回线
  • 图像：
    • 铁磁材料的磁导率是多值的。
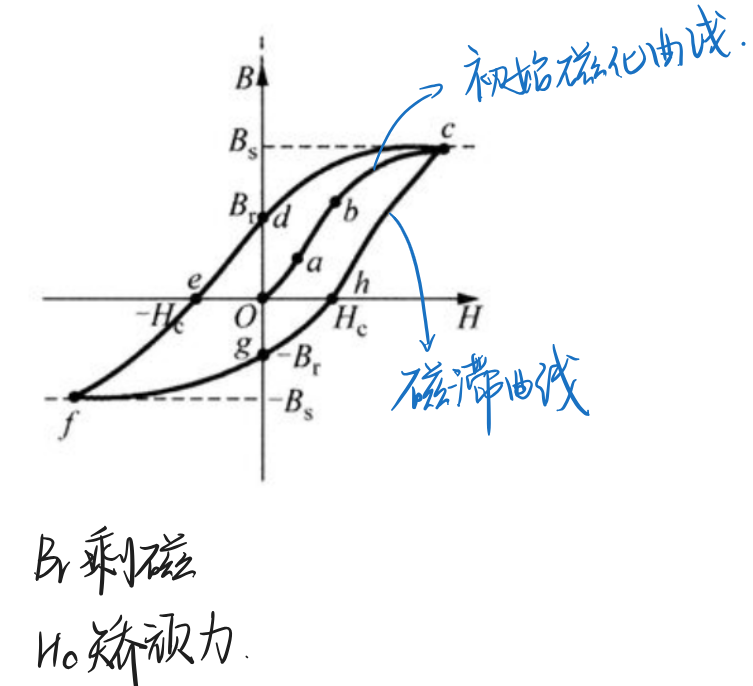
  • 现象解释：磁畴。
  • 当铁磁材料温度高于居里温度时，铁磁材料会表现出和顺磁材料相同的磁化性质。
  • 消除永久磁铁的磁性的方法：升温/等待or碰撞/把磁铁放入交变磁场中。
  • 材料
    • 软磁：矫顽力$H\_{c}$小。磁滞损耗小。易于磁化也易于退磁。eg：铁硅合金（硅钢片）
    • 硬磁：矫顽力$H\_{c}$大。剩磁较强，又称永磁材料。
      • 矩磁：磁滞回线类似长方形，可以传递信息。

电磁感应

• 楞次定律

$$\epsilon=-\frac{d\left( \sum \Phi_{m} \right)}{dt}$$

$n$匝线圈（磁通量相同）

$$\epsilon=-N \frac{d\Phi_{m}}{dt}$$

• 动生电动势：因洛伦兹力产生 场强（推理）：

$$\vec{E}\_{k}=\frac{\vec{F}\_{m}}{-\mid e \mid}=\vec{v} \times \vec{B}$$

动生电动势：

$$\epsilon=\oint_{l}(\vec{v}\times \vec{B})\cdot d \vec{l}$$

（注意：后面是点乘哦！！） 注意，这里仍然可以用化曲为直的trick 长度为$L$和半径为$L$的导体圆盘的电动势

$$\epsilon=\frac{1}{2}BwL^2$$

电动势的正负由电流的正负来判断。 在机械能转化为电能的时候，洛伦兹力起到了中间媒介的作用。

• 感生电动势：因磁场发生变化而产生(注意其中的负号)

$$\epsilon=\oint\_{l} \vec{E}\_{i}\cdot d \vec{l}=-\iint\_{S} \frac{\partial\vec{B}}{\partial t} \cdot d \vec{S}=- \frac{d\Phi\_{m}}{dt}$$

$\vec{E}_{i}$是感应电场。与静电场不同的是，它对任意闭合回路的环流一般不为零。感应电场是一种有旋场。 上式也可写成：

$$\nabla \times \vec{E}_{i}=-\frac{\partial \vec{B}}{\partial t}$$

• 变化磁场中的闭合导体回路的总电动势

$$\epsilon=\oint\_{l}(\vec{v}\times \vec{B}) \cdot d \vec{l}+\oint \vec{E}\_{i} \cdot d \vec{l}=\oint\_{l}(\vec{v}\times \vec{B}) \cdot d \vec{l}-\iint\_{S} \frac{\partial\vec{B}}{\partial t} \cdot d \vec{S}$$

• 电子感应加速器中电子轨道上的磁感应强度和轨道内磁场磁感应强度的平均值的关系

$$B=\frac{1}{2}\bar{B}$$

• 自感：线圈回路电流发生变化时，引起穿过自身回路的磁通量发生变化。自感线圈可以扼制高频电流通过。
• 自感系数（定义式）

$$\Psi=LI$$

（$\Psi$为线圈自身的磁通匝链数，$L$是线圈的自感系数） （计算时要注意，磁场的方向与电流的方向是垂直的） 单位：亨利$H$，单位$Wb/A$，$mH-10^{-3}$，$\mu H-10^{-6}$

• 自感电动势（定义式）：

$$\epsilon_{L}=-\frac{d\Psi}{dt}=-L \frac{dI}{dt}-I \frac{dL}{dt}$$

这个式子的含义：线圈中电流变化→线圈磁通量变化→引发感应电动势：感应电动势方向与电流变化方向相反，也与电流引起的磁通量变化相反。 在有的题目中，外磁场变化导致线圈中电流的变化。这个时候，利用不带负号的另一个公式：

$$\frac{d\Psi}{dt}=-L \frac{dI}{dt}$$

这个式子的含义：外磁场变化→线圈磁通量变化→引发感应电动势（15-20（2））

• 螺线管的自感系数

$$L=\mu_{0}n^2V$$

$n=\frac{N}{l}$，单位长度螺线管的匝数。$V=lS$，螺线管内空间的体积。

• 利用磁场能计算自感系数

$$L=\frac{2W_{m}}{I^2}$$

• 互感：不同线圈之间相互感应。
• 互感系数

$$\Psi_{21}=M I_{1}$$

$I_{1}$是1线圈通过的电流，$\Psi_{21}$是1线圈电流对2线圈中磁通量的变化影响。

• 互感电动势

$$\epsilon_{12}=-M \frac{dI_{2}}{dt}-I_{2} \frac{dM}{dt}$$

• 自感与互感电动势之间的关系

$$M=k \sqrt{ L_{1}L_{2} }$$

$k$是耦合系数，$0<k \le 1$，耦合系数为$1$时，称线圈中有完全的磁耦合。 计算自感/互感系数时，均以元件自感的磁通量方向为正方向（例15-13）

• 线圈载流$I_{0}$时，线圈激发出磁场的能量

$$W_{m}=\frac{1}{2}L I_{0}^2$$

来源：接通电流时，电源电动势反抗线圈自感电动势所做的功。

• 长直螺线管磁场能量

$$W_{m}=\frac{1}{2} \frac{B^2}{\mu}(Sl)$$

• 磁场的能量密度（也称磁压）

$$w_{m}=\frac{1}{2} \frac{B^2}{\mu}=\frac{1}{2}BH$$

注意：在考虑磁场方向的时候，$B$是矢量。

• 磁场总能量和磁场能量密度之间的关系

$$W_{m}=\iiint_{\Omega}w_{m}dV=\iiint_{\Omega} \frac{1}{2} \frac{B^2}{\mu}dV$$

磁场力做负功，磁场能增加。（15-32）

• 两个通入不同电流的线圈的磁场能量

$$W_{m}=\frac{1}{2}L_{1} I_{1}^2+\frac{1}{2}L_{2}I_{2}^2\pm MI_{1}I_{2}$$

• 计算两个通入不同电流的线圈的磁场能量：利用磁场能来源于线圈对电源电动势的反抗这一点求出。（例15-15）
• 自感磁能总是正的，互感磁能可能大于$0$，也可能小于$0$
• 在一个有感应电动势和电阻的电路中计算两点的电势差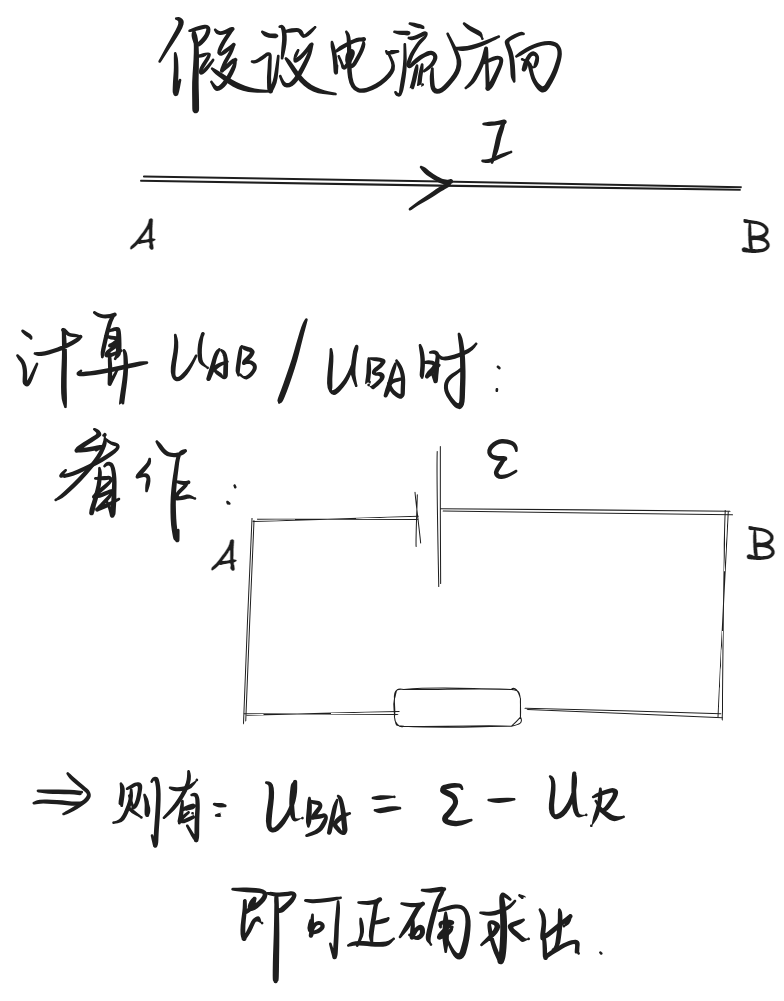： (15-8、15-15、15-25)
• 若参与自感/互感的线圈是闭合线圈，则有

$$-L_{1} \frac{dI_{1}}{dt}-M\frac{dI_{2}}{dt}=0$$

机械波

• 波速、波长与频率

$$\lambda=uT$$ $$\lambda \nu=u$$

• 一维平面简谐波表达式（沿x轴正方向）

$$y=A\cos\left[ w\left( t-\frac{x}{u} \right)+\phi_{0} \right]$$

化简得

$$y=A\cos(wt-kx+\phi_{0})$$

同理：沿x轴负方向传播的波

$$y=A\cos(wt+kx+\phi_{0})$$

其中：$k=\frac{2\pi}{\lambda}$，也即$2\pi$长度内包含的完整波的个数 在计算不同点的相位时，注意根据方向与波程差具体问题具体分析

• 波传播方向上两点的相位差

$$\Delta \phi=k\Delta x$$

• 要保证波的振动状态确定，则需要保证：$wdt=kdx$，也即波速恒定。
• 弦的波动方程

$$\frac{\partial^2y}{\partial t^2}=v^2\frac{\partial^2y}{\partial x^2}$$

证某个式子是不是它的解：对$x$，$t$两个分量分别求偏导。

• 平面简谐波中质元的能量

$$\Delta E=\Delta E_{k}+\Delta E_{p}=\Delta mw^2A^2\sin^2(wt-kx)$$

（势能的计算：将水平方向的拉力看作竖直方向的（因为太小了）） 质元位于平衡位置附近：具有最大动能/势能/机械能；位于最大位移附近：反之。 质元在波动过程中机械能不守恒。 单位体积介质具有的能量（能量密度）

$$w=\rho w^2 A^2 \sin^2(wt-kx)$$

动能：

$$E_{k}=\int \frac{1}{2}\rho \left( \frac{\partial y}{\partial t} \right) ^2\, dx$$

势能：

$$E_{p}=\int \frac{1}{2}\rho u^2\left( \frac{\partial y}{\partial x} \right)^2 \, dx$$

在一个周期内的平均值

$$\bar{w}=\frac{1}{2}\rho w^2A^2$$

在以上几式中，$\rho$是弦的线密度$\frac{\Delta m}{\Delta x}$。

• 能流：单位时间内波通过与传播方向相垂直的某一面积的能量，单位$J/s$，其中$w$是能量。

$$P=uwS$$

平均能流：$P=U \bar{w}S$

$$\bar{P}=\vec{I}\cdot \vec{S}$$

如果介质没有吸收能量，则通过不同波面的能量相等。

• 波的强度/能流密度（单位$W/m^2$）：

$$I=\frac{\bar{P}}{S}$$

• 注意能量密度和能流密度的区别。
• 声波频率范围：$20Hz\sim 20kHz$
• 声强（与特定的声波频率有关）： $1000Hz$闻阀为标准声强$I_{0}=10^{-12}W/m^2$
• 声强级

$$L=10\lg \frac{I}{I_{0}}$$

单位为$dB$

• 波的折射定律

$$\frac{\sin i}{\sin r}=\frac{u_{1}}{u_{2}}$$

$i$为入射角；$r$为反射角

• 波的干涉（要求：频率相同，振动方向相同，相位差恒定） 相位差：

$$\Delta \phi= \phi_{2}-\phi_{1}-k(r_{2}-r_{1})$$

振幅（方法：矢量图叠加）：

$$A=\sqrt{ A_{1}^2+A_{2}^2+2A_{1}A_{2}\cos\Delta \phi }$$

当$\Delta \phi=\pm2n \pi$（$n$为自然数）时：和振幅最大，干涉相长点。 当$\Delta \phi=\pm(2n+1)\pi$（$n$为自然数）时：和振幅最小，干涉相消点。 若初相位相等：干涉相长：$\pm n\lambda$；干涉相消：$\pm(2n+1)\frac{\lambda}{2}$ 相邻同性点间距：$\lambda$ 相邻异性点间距：$\frac{\lambda}{2}$ （注意波程差的正负）

• 驻波：两列振幅相同的相干波在一直线上沿反方向传播，产生干涉

$$y=2A\cos kx\cos wt$$

$x=\pm n \frac{\lambda}{2}$（$n$为自然数），质元振幅最大，称为波腹 $x=\pm (2n+1) \frac{\lambda}{4}$（$n$为自然数），保持静止，称为波节 相邻同性点间距：$\frac{\lambda}{2}$ 相邻异性点间距：$\frac{\lambda}{4}$ 能量变化： 当所有质元均处于平衡位置时：驻波的能量仅为质元的动能。其中波节处由于速度为0，能量密度为0，而波腹处由于速度最大，能量密度最大。 当所有质元均处于最大振幅位置时：驻波的能量仅为质元的势能。其中，波节处由于导数最大，所以相对位移最大，因此能量密度最大；波腹处由于导数最小，所以相对位移最小，因此能量密度最小。 每隔$\frac{1}{4}$周期，驻波能量发生转化，能流在波腹和波节之间流动。 注意：波节处是振动势能为$0$的地方。 注意$n$个波节之间的植树问题

• 在弦上形成驻波
  • 固定张紧的弦中形成驻波：$l=n \frac{\lambda}{2}$，（$n$为不等于$0$的自然数）；频率：$\nu=\frac{n}{2l}u$。$n=1$，基频/基音/简正频率；其他，$n$次谐频/泛音/固有频率
  • 一段固定，一段自由：$l=n \frac{\lambda}{2}+\frac{\lambda}{4}$，（$n$为不等于$0$的自然数）；频率：$\nu=\frac{2n+1}{4l}u$
• 波阻抗

$$Z=\rho u$$

$Z$是波阻抗；$\rho$是密度；波速是$u$。较大的称为波密介质，较小的称为波疏介质。

• 相位突变：
  • 若驻波由波的反射产生，且反射点是波节，反射波和入射波之间存在着$\pi$（或者是$\frac{\lambda}{2}$，但绝不是$\frac{\pi}{2}$或者$\lambda$）的相位差
  • 反射端是自由端，不会发生
  • 波从波疏介质入射到波密介质，垂直入射或者掠入射，反射光有半波损失。
  • 波从波密介质入射到波疏介质反射不会出现
• 多普勒效应

$$\nu_{R}=\frac{u'}{\lambda'}=\frac{u\pm v_{R}}{u\mp v_{S}}\nu$$

分母代表波源，分子代表接收器。二者靠近，频率增大；二者远离，频率减小。 若介质流动的速度为$v_{m}$，则波速变为$u\pm v_{m}$

• 同方向不同频率振动的叠加 和振动

$$x=x_{1}+x_{2}=2A\cos\left( \frac{w_{1}-w_{2}}{2}t \right)\cos\left( \frac{w_{1}+w_{2}}{2}t+\phi \right)$$

振幅变化的频率称为拍频

$$\Delta \nu=\frac{\mid w_{1}-w_{2}\mid}{2\pi}=\mid \nu_{1}-\nu_{2}\mid$$

电磁场

• 电容器中的位移电流

$$i_{d}=C \frac{du}{dt}$$

• 麦克斯韦方程组（理论上来说，记住了这个方程组就可以做所有题）

$$\int\kern{-8pt}\int \kern{-23mu} \bigcirc_{S} \vec{D} \cdot d \vec{S}=\iiint_{\Omega}\rho_{0} dV$$ $$\int\kern{-8pt}\int \kern{-23mu} \bigcirc_{S} \vec{B} \cdot d \vec{S}=0$$ $$\oint_{l} \vec{E} \cdot d \vec{l}=-\iint_{S} \frac{\partial \vec{B}}{\partial t} \cdot d \vec{S}$$ $$\oint_{l} \vec{H} \cdot d \vec{l}=\iint_{S}(\vec{j}_{c}+ \frac{\partial\vec{D}}{dt}) \cdot d \vec{S}$$

（注：位移电流注意方向）

$$\vec{F}=q \vec{E}+q \vec{v}\times \vec{B}$$ $$w=w_{e}+w_{m}=\frac{1}{2}\epsilon E^2+\frac{1}{2\mu}B^2$$

注意传导电流是电路中的还是别的地方的，同时要注意传导电流的正负。 同时注意，电磁场中磁场分量不存在半波损失。（16-9）

• 电场磁场满足的偏微分方程

$$\nabla ^2 \vec{E}=\mu \epsilon \frac{\partial^2 \vec{E}}{\partial t^2}$$ $$\nabla ^2\vec{H}=\mu \epsilon \frac{\partial^2 \vec{H}}{\partial t^2}$$

传播速度

$$c=u=\frac{1}{\sqrt{ \mu \epsilon }}$$

真空中

$$u=\frac{1}{\sqrt{ \mu_{0} \epsilon_{0} }}$$

介质中

$$u=\frac{c}{n}$$

• 电磁波电磁分量的关系 振幅：

$$\sqrt{ \mu }H_{0}=\sqrt{ \epsilon }E_{0}$$

频率/相位：相同 $(\vec{E}\times \vec{H})// \vec{u}$

• 电磁波的能流密度：坡印廷矢量$\vec{S}$

$$S=wu$$

矢量表达式

$$\vec{S}= \vec{E} \times \vec{H}$$ $$S=\sqrt{\frac{\epsilon_{0}}{\mu_{0}} }E^2=\sqrt{ \frac{\mu_{0}}{\epsilon_{0}} }H^2$$

同时注意，这里的$E$和$H$是可变量。由坡印廷矢量算得的$E$和$H$一般是平均值。 计算电磁场的平均强度：

$$I=\bar{S}=\frac{1}{2}E_{0}H_{0}$$

（注意，$E_{0}$与$H_{0}$是最大值）

• 电磁波的物质性

$$\frac{d}{dt}\iiint_{\Omega}wdV=-\int\kern{-8pt}\int \kern{-23mu} \bigcirc_{A} \vec{S}\cdot d \vec{A}$$

• 导体平板表面（$\Delta A$）受到电磁波的作用力

$$\vec{F}= \frac{\vec{S}-\vec{S'}}{c}\Delta A$$

入射电磁波$\vec{S}$，反射电磁波$\vec{S'}$ 电磁波的动量变化

$$\Delta \vec{P}= \frac{ \vec{S'}-\vec{S}}{c}\Delta A \Delta t$$

• 单位体积内电磁场对应的动量（电磁波的动量密度）

$$\vec{g}= \frac{\vec{S}}{c^2}$$

• 电磁波的质量密度

$$m=\frac{w}{c^2}$$

由$\vec{S}=w \vec{u}$可以推出电磁波动量密度的公式。

• 有关$LC$振荡电路的一些方程

$$\frac{d^2q}{dt^2}+\frac{1}{LC}q=0$$

线路中的磁场能量：

$$W=\frac{q_{0}^2}{2C}$$

振荡频率：

$$w=\frac{1}{\sqrt{ LC }}$$

振荡电路退化成一根直导线，称为振荡电偶极子。类似广播电台的天线。

• 电磁波 长波/中波/短波：无线电广播通信（前两者：地波；后两者：天波） 米波/分米波：电视、导航、移动通信 厘米波/毫米波：称为微波 红外线/可见光/紫外线/X射线/γ射线

光的干涉

• 插播一条：折射定律

$$\sin \theta_{1} \cdot n_{1}=\sin \theta_{2} \cdot n_{2}$$

• 光的非相干叠加

$$I=I_{1}+I_{2}$$

• 光的相干叠加

$$I=I_{1}+I_{2}+2\sqrt{ I_{1}I_{2} }\cos \Delta \phi$$

若$I_{1}=I_{2}$

$$I=4I_{1}\cos^2 \frac{\Delta \phi}{2}$$

两组相干光进行非相干叠加的相位差相差为$\pi$时，条纹消失。（例17-6）

• 光程差

$$\delta=n_{1}r_{1}-n_{2}r_{2}$$

• 杨氏干涉（波阵面分割法） 光强分布

$$I=4I_{0}\cos^2\left( \frac{\pi d}{\lambda} \frac{\Delta x}{L} \right)$$

干涉明条纹

$$x_{m}=\pm m \frac{L\lambda}{d}$$

（$m$是自然数） 干涉暗条纹

$$x_{m}=\frac{\pm(2m-1)L\lambda}{2d}$$

（$m$是除$0$之外的自然数）（注意，这里是相减，可以得出一个结论：第$n$条明条纹中心跟第$n$条暗纹中心相差$\frac{\lambda}{2}$，并且暗条纹比明条纹更接近中心。） （洛埃镜，由于半波损失，所以明暗条纹的位置与杨氏的相反） 若光源不在两狭缝的正中，而是距狭缝的正中距离为$X$，光源距狭缝距离为$D$，则

$$\delta=\left( \frac{X}{D}+\frac{x}{L} \right)d$$

明条纹位置

$$x_{m}=\pm m \frac{\lambda L}{d}-\frac{XL}{D}$$

（$m$为自然数） 当光源宽度为$b$，错开的距离$\frac{bL}{D}$。当$\frac{bL}{D}=\frac{\lambda L}{d}$时，干涉条纹消失。所以要求光源宽度$b< \frac{D\lambda}{d}$，狭缝间距$d_{min}< \frac{D\lambda}{b}$，其中$d_{min}$是相干距离。 非单色光，光程差增加到$L_{max}$时，干涉条纹刚好消失

$$L_{max}=\frac{\lambda_{0}^2}{\Delta\lambda}$$

$\lambda_{0}$为中心波长，$\Delta\lambda$为光波的线宽。

• 干涉条纹的可见度

$$V=\frac{I_{max}-I_{min}}{I_{max}+I_{min}}=\frac{2\sqrt{ I_{1}I_{2} }}{I_{1}+I_{2}}$$

或令这两组相干光相位差相差为$\pi$（17-6）

• 薄膜干涉（分振幅法） 等倾干涉（厚度均匀的薄膜） 光程差由入射角决定

$$\delta=2d\sqrt{ n_{2}^2-n_{1}^2\sin^2i }+\frac{\lambda}{2}$$

入射角相同，形成的条纹会重叠在一起 $i$越大，干涉级越低 等厚干涉（厚度不均匀的薄膜） 劈形膜 $e$为膜的厚度，劈的角度为$\alpha$ 光程差为

$$\delta=2ne+\frac{\lambda}{2}$$

相邻条纹的间距

$$l=\frac{\lambda}{2n\alpha}$$

牛顿环 光程差

$$\delta=2e+\frac{\lambda}{2}$$

其中

$$e=\frac{r^2}{2R}$$

曲率半径

$$R=\frac{1}{K\lambda}(r_{m+k}^2-r_{m}^2)$$

迈克尔孙干涉仪 消除了半波损失的影响 连续移过$N$个干涉条纹（间距为$N\lambda$，也就是相位差）时，$M_{1}$产生的移动$N \frac{\lambda}{2}$ 在迈克尔逊干涉仪中，屏幕上干涉条纹的间距与薄膜的厚薄程度有关（17-21）。

• 天线阵（例17-9）发射的电磁波强度

$$I=I_{0}\left[ \frac{\sin\left( \frac{N\Delta \phi}{2} \right)}{\sin\left( \frac{\Delta \phi}{2} \right)} \right]^2$$

其中$\Delta \phi=kd\sin\theta-\Delta \psi$，其中$\Delta \psi$是两个相邻振子之间的相位差。 在沿天线阵的排列方向上发射的电磁波最强 条纹的左移和右移，向哪里运动：看同一级条纹的变化。

光的衍射

• 菲涅耳衍射：衍射屏与光源、观察屏间距有限远。
• 夫琅禾费衍射：衍射屏和观察屏的距离是无限远

单缝夫琅禾费衍射

• 光强分布

$$I=I_{0}\left( \frac{\sin\beta}{\beta} \right)^2$$

$\beta=\frac{\pi a}{\lambda}\sin\theta$，其中$a$是狭缝宽度，$f$是透镜焦距，也就是透镜到观察屏的距离。

• 暗条纹位置：

$$a\sin\theta=\pm m\lambda$$

• 明条纹位置：

$$\theta=0$$

以及

$$a\sin \theta=\pm(2m+1) \frac{\lambda}{2}$$

（记忆：菲涅耳半波带法）

• 中央明条纹宽度

$$\Delta x=\frac{2\lambda f}{a}$$

要产生明显的衍射现象，缝宽应与波长相近。

双缝夫琅禾费衍射（干涉+衍射）

• 光强分布（干涉条纹受衍射条纹的调制）

$$I=4I_{0}\left( \frac{\sin\beta}{\beta} \right)^2 \cos^2\left( \frac{\pi d}{\lambda}\sin\theta \right)$$

• 列阵定理：光强分布函数是衍射光强分布函数与干涉光强分布函数的乘积

圆孔衍射

• 第一级暗条纹

$$\theta_{0}\approx\sin\theta_{1}=1.22 \frac{\lambda}{d}$$

（$d$是圆孔的直径，$\theta_{0}$为艾里斑的角半径，$R=f\theta_{0}$为艾里斑的半径）

• 瑞利判据：一个点光源的衍射图样恰好与另一个点光源的衍射图样的第一个最暗处重合，规定此时这两个点光源恰好可以为这光学仪器分辨。
• 圆孔型透镜的最小分辨角（仪器的分辨本领）=艾里斑的角半径。
• 提高光学仪器分辨本领：增大直径/采用较短的波长

光栅衍射（与光线通过$n$个缝的干涉不同）

缝宽$a$、缝间距$b$、光栅常数$d$、狭缝数$N$

• 光强分布

$$I=I_{0}\left( \frac{\sin\beta}{\beta} \right)^2\left( \frac{\sin N{\frac{\Delta \phi}{2}}}{\sin\frac{\Delta \phi}{2}} \right)^2=I_{0}\left( \frac{\sin\beta}{\beta} \right)^2\left( \frac{\sin N\alpha}{\sin\alpha} \right)^2$$

前面是衍射项，后面是干涉项。 $\Delta \phi=kd\sin\theta$

• 干涉项： 主极大（$\alpha=m\pi$，$m$是自然数时，取极大值）

$$d \sin \theta_{m}=\pm m \lambda$$

$\sin \theta_{max}=1$ （这个同时也是光栅的光栅方程） 暗纹（$\sin N \alpha=0$且$\sin\alpha\ne{0}$，$m$为不为$0$的自然数且$m\ne N,2N,\cdot\cdot\cdot$）

$$d\sin\theta_{m}=\pm \frac{m}{N}\lambda$$

• 衍射项： 单缝衍射极小（其中$m$是除$0$之外的自然数）

$$a\sin \theta=\pm m \lambda$$

• 缺级条件：单缝衍射极小和主极大同时成立。

$$a=\frac{d}{m}$$

（$a$是缝宽，$d$是光栅常数，$m$是主极大缺级的极数）

• 光栅的分辨本领 条件：瑞利判据

$$m\lambda=\frac{mN-1}{N}(\lambda+\Delta\lambda)$$ $$R=\frac{\lambda}{\Delta\lambda}=mN-1\approx mN$$

若$\frac{\lambda}{\Delta\lambda}>mN$，则可以分辨。（17-32）

• 正弦光栅的通过率

$$A(X)=1+\cos\left( \frac{2\pi X}{d} \right)$$

$d$是光栅常数，也称空间周期。空间周期越小，条纹间距就越大。 黑白光栅可以看书哦是具有不同空间频率的正弦光栅的叠加。

X射线衍射

呃，其实其原理是干涉... 假设原子层之间的距离为$d$，则散射射线形成亮点的条件是

$$2d\sin\theta=m\lambda$$

$\theta$是光线与原子层的夹角。 注意：在写式子的时候，要考虑处理的是$\cos$的还是$\cos^2$

光的偏振

• 线偏振光：光振动矢量$E$保持在确定的平面内，偏振面为一直线。
• 椭圆/圆偏振光：迎着光传播方向，顺时针右旋，逆时针左旋；看作两个相互垂直，存在确定相位差的偏振光叠加而成 （相关合成：画图）
• 自然光：可分解为两个振动方向垂直，等幅，不相干的线偏振光
• 部分偏振光：光矢量振动方向不具有轴对称分布
• 马吕斯定律：

$$A_{2}=A_{1}\cos\alpha$$ $$I_{2}=I_{1}\cos^2\alpha$$

$\alpha$是入射光矢量的振动方向和偏振片偏振化方向的夹角；$A_{1}$，$A_{2}$是入射，出射光的振幅；$I_{1}$，$I_{2}$则是相应的光强。

• 自然光透过偏振片之后光强如果小于$0.5I_{0}$，说明偏振片有吸收
• 布儒斯特定律 当入射角$\theta_B=\arctan \frac{n_{2}}{n_{1}}$（别反了）（也就是，反射光和折射光之间夹角为$\frac{\pi}{2}$的时候），反射光为振动方向垂直于入射面的线偏振光，折射光是部分偏振光。利用多层介质（如堆叠的玻璃片）可以使得折射光为振动方向在入射面内的线偏振光，反射光为垂直于入射面的线偏振光） 写相关式子的时候，最好不要写比值式，而是写连等式。
• 检验偏振
  • 通过并旋转偏振片
    • 光强不变：自然光/圆偏振光
      • 有变化，无消光位置：部分偏振光/椭圆偏振光
      • 有变化，有消光位置：线偏振光
  • 通过四分之一波片：区分自然光/圆偏振光
  • 转动偏振片寻找椭圆的长短轴→四分之一波片光轴对椭圆长轴（椭圆偏振光这时变为线偏振光，因此可以判断）

晶体的双折射

• 光轴：晶体中的一个方向，光线在该方向传播不产生双折射；但是如果从晶体外沿光轴方向入射，则会产生双折射。
• $o$光的主平面：$o$光和光轴所在平面
• $e$光的主平面：$e$光和光轴所在平面
• $o$光：寻常光，遵守折射定律，线偏振光，方向垂直于其所在主平面，与光轴的夹角恒定，因此速率确定，晶体折射率确定
• $e$光：非常光，不遵守折射定律，线偏振光，方向在其主平面内，与光轴的夹角各异，因此速率不确定，发出波面为椭球面。沿垂直于晶体光轴方向传播时，折射率称为非常光的主折射率$n_{e}$；沿光轴方向传播时，折射率与寻常光相等。
• 两个子波面在光轴上相切，在垂直光轴的方向上，速率相差最大。
• 光轴平行于晶体表面，且有平行光入射时，由于两束光传播速度不一致，所以存在光程差。 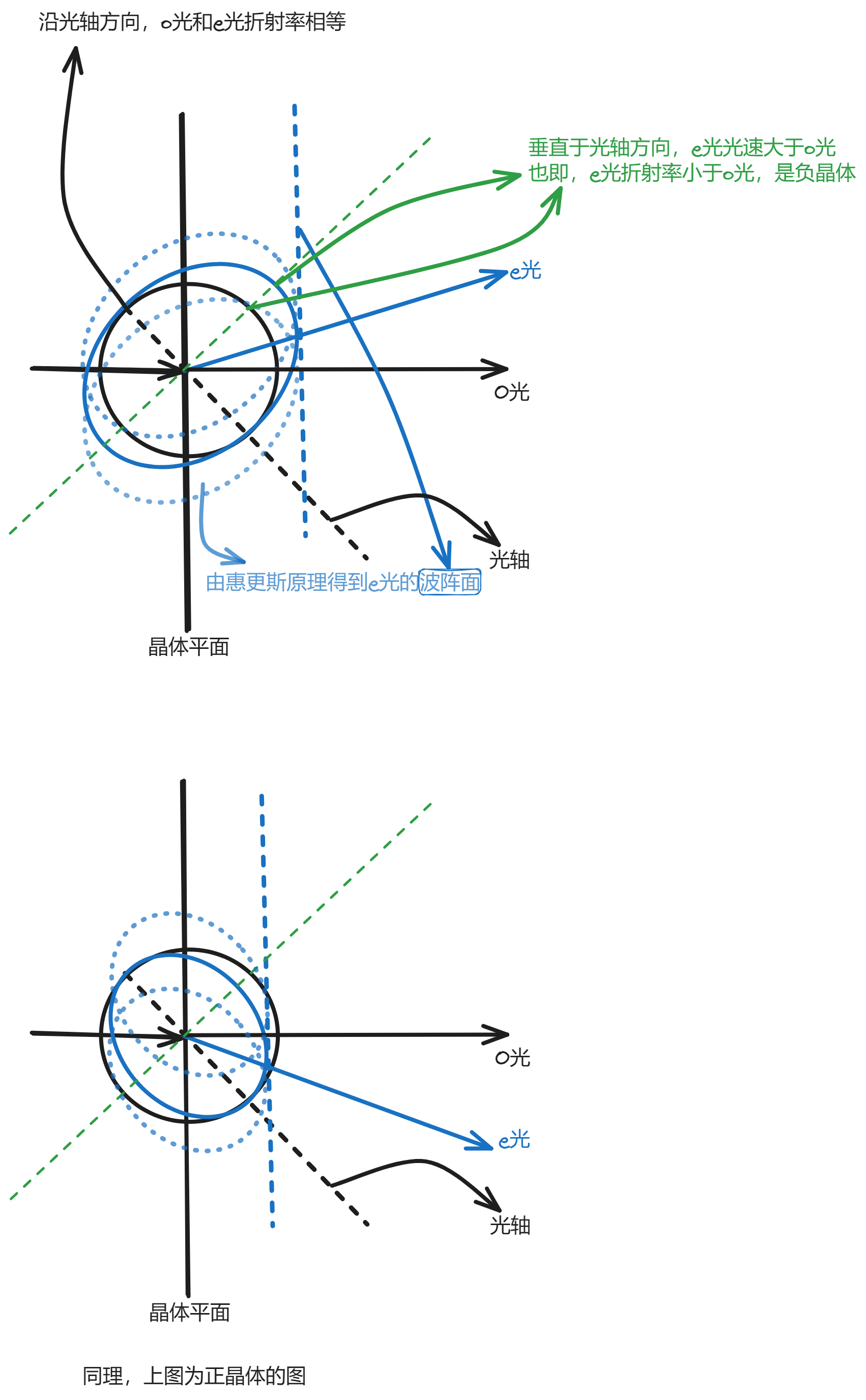两束光的相位差

$$\Delta \phi=\frac{2\pi}{\lambda}\delta=\frac{2\pi}{\lambda}(n_{o}-n_{e})d$$

使出射光相位差$\Delta \phi=\frac{\pi}{2}$（也就是$\frac{\lambda}{4}$）的晶体片称为四分之一波片，还有二分之一波片，均针对特定的波长。

• 应用：注意不要弄混
  • 线偏振光通过四分之一波片，使得线偏振光变为椭圆（变成圆偏振光需要入射的线偏振光的振动方向与光轴成$\frac{\pi}{4}$角）
  • 线偏振光通过二分之一波片，使得线偏振光的振动方向转过$2\alpha$角，$\alpha$是入射偏振光振动方向与光轴之间的夹角。
• 注意：偏振方向相反（相差180°）的两束光可以等效为两束相位差为$\pi$的光
• 原因：晶体结构的各向异性导致介电常数在不同方向的值不同

注意

提示

• 位移电流注意正负
• 等厚干涉注意二倍关系！
• 明暗条纹的判断：使用$\frac{a}{d}=m$的时候注意是缺级的。
• 均匀带电的长直圆柱面：看作螺线管即可
• 最高级次：代入$\sin \frac{\pi}{2}=1$
• 光学注意相位
• 一定要注意：$I=E^2$
• $F=-\frac{dW_{m}}{dx}$（把磁场密度看作压强）