数字电子技术
绪论
- 数字对应“离散”,模拟对应“连续”
- 关注离散的电信号
- 电子技术:研究电子器件/电子器件应用
- 电子电路:处理信息,能量转换
- 模拟电路:用连续的模拟电压、流值来表示信息
- 数字电路:用离散的电压序列来表示信息
- 结构
- 按层次,每个层次有确定的复杂度
- 复用
- 接口
- 隔离系统
- 系统具有良好的扩展与外设性
- 好的设计
- 最少的技术达到最大的功效
- 可靠性
- 兼容性
信息和编码:编码的目的和二进制编码
- 用离散的电压序列��来表示
- 信息编码:香农公式 假设你有n种等可能的选择,之后将它们缩减为m种等可能的选择。那么我给了你比特的信息。
- 编码:对信息进行描述与代表,要保证信息的唯一性
- 数制(二进制)
- 二进制的补码:产生的原因是:如果用某一位数来表示二进制符号位的话,码的运算规则和数的运算规则发生了冲突;不对称的原因是有的存在;小数点补码取值方法:的时候,在二进制的最末一位即可;相当于是考试中的“算负分”
- 码制(二值逻辑)
- 等长编码(需要等可能)
- eg:十进制/ASCII码
- 编码方式不唯一依据应用背景与物理条件形成。举例如下:
- 余3码用来解决进位(使得进位后的数字也在那个数字的范围内)的问题(要修正)
- 格雷码相邻代码只有一位改变状态,每一位的状态变化都按一定的顺序循环——可以将物理距离用不同编码的个数表示出来(网路路由器的编码)
- 变长编码(不等可能)
- 频繁出现的,用短编码;不频繁出现的,用长编码
- 假设为事物出现的频率,那么信息量比特;平均编码长度为:
- 哈夫曼编码(使用哈夫曼树):前提,知道统计规律
- 等长编码(需要等可能)
- 数制(二进制)
逻辑代数基础
- 逻辑运算
- 方式:and(表达式),or(表达式),not(读图时,只要有圈圈就取反)
- 获得逻辑关系:编码
- 表示逻辑关系(在确定的逻辑关系的情况下,获得的结果是有限的):真值表
- 复合逻辑运算
- 与非
- 或非
- 与或非(两个与门汇集到一个或门上,再取非)
- 异或(表达式)
- 同或(表达式)
- 基本公式
- 其中前两个式子被称为德摩根定理
- 常用公式(用真值表均可证明,这里给出部分公式的推演过程)
- (使用可以推出)
- (证明:,之后展开)(同理也成立,换为其他杂项也可)
- ,
- 逻辑式的长短可能与电路的简洁与否有关
- 基本定理
- 代入定理:在任何一个包含的逻辑等式中,若以另外一个逻辑式代入式中的位置,则等式依然成立(可以让公式变得千变万化!)
- 反演定理:对任意逻辑式,把与变成或,或变成与,原变量变成反变量,反变量变成原变量。
- 变换顺序:先括号,然后与,最后或
- 例子:
- 在数字电路实现过程中意义不大
- 对偶定理:与变成或,或变成与,1变成0,0变成1
- 逻辑函数及其表示方法
- 表达方法(采用不同编码方式,可以相互转换):真值表(描述是确定的),逻辑式(抽象程度最高),逻辑图(跟电路图相似程度最高),波形图(可以实际观测得到),卡诺图,EDA中硬件描述语言
- 不同的表达方法可以相互转换
- 真值表逻辑式相互转换:将结果为1的行取出:同一行不同列用“与”连接;不同行之间用“或”连接
- 逻辑式真值表:先消去没用的变量
- 逻辑图逻辑式:一条一条画,然后化简
- 真值表可以有多个输出端(真值表增加一列) ;输出可能性的个数为,但不一定要遍历,输入端一定遍历
- 波形图:将输入变量所有取值可能与对应输出按时间顺序排列起来,画成时间波形。(寻找电路变化的最小周期,看看有没有那么多种可能性,若电路图观测完整,寻找输出为1/0(哪个方便写哪个,取0可以取反)对应的输入值)
- 逻辑函数的两种标准形式
- 最小项之和(利用“与”的关系,在获得1比较困难的时候,获得结果为1的一行)
- 定义
- m是乘积项
- 包含n个因子
- n个变量均以原变量和反变量的形式在m中出现一次
- 的最小项
- 编码方式:取值为1时,相应变量取值对应的二进制数(取到为1,没取到为0)
- 最小项性质:
- 在输入变量任意取值下,有且仅有一个最小项的值为1
- 全体最小项之和为1(遍历了所有的取值)
- 任何两个最小项之积为0
- 两个相邻的最小项之和(如:与)可以合并,消去一对因子
- 任何一个函数都可以化为最小项之和
- 利用公式,可以将任意一个函数化为最小项之和
- 定义
- 最大项之积(利用“或”的关系,在获得1比较容易的时候,获得结果为1的一行
- 最大项(最小项取反):利用德摩根公式,化为
- 定义
- M是相加项
- 包含n个因子
- n个变量均以原变量和反变量的形式在M中出现一次
- 编码方式:取值为0时,相应变量取值对应的二进制数
- 证明:最小项之和剩下最小项之和,之后取反使用德��摩根定律获得
- 同一个函数用最小项之和和最大项之积分别表示,可以将函数中涉及到的变量的正反符号全部用光,形成了“互补”关系
- 最小项之和(利用“与”的关系,在获得1比较困难的时候,获得结果为1的一行)
- 逻辑函数的化简法
- 逻辑函数的最简形式:最简与或,包含的乘积项已经最少,每个乘积项的因子也最少
- 公式化简法
- (最后一步,出现了B的原变量和反变量,见常用公式)
- 卡诺图化简法
- 将逻辑函数的最小项之和的以图形的方式表示出来
- 个小方块分别代表n变量的所有最小项,排列成矩阵,使得几何位置相邻的最小项在逻辑上也是相邻的,就得到最小项的卡诺图
- 3变量的卡诺图(为保证相邻,可以看作向右展开) 图见:认识卡诺图_三变量卡诺图_ccoolllaaa的博客-CSDN博客类似于格雷码,卡诺图在(立体)几何上也是相邻的 (折叠啊折叠)
- 局限:�变量不能太多
- 卡诺图化简
- 化为最小项之和/从逻辑式直接填
- 卡诺图上最小项对应的位置填1,其他填0
- 依据具有相邻性的最小项可以合并,消去不同因子
- 原则(判断相邻的时候,注意“穿墙而过的”)
- 两个相邻最小项可以合并为一项,消去一对因子
- 四个-两对
- 八个-三对
- 画大不画小
- 项数最少,每项因子最少
- 画圈可以叠加,但每个圈都要有新鲜的1
- 应该覆盖所有的1
- 不能拐弯,不是消消乐(大雾)
- 也可以圈0,取反即可
- 两个变量的卡诺图,不能化简的:异或/同或,对角线;3变量最多含有4个不能化简的最小项(对角线);4变量最多8个(也是走对角线);n个变量最多个
- 化简结果不唯一,但个数一样(画圈大小/个数相同)
- 具有无关项的逻辑函数化简
- 无关项
- 约束项:对一些量的输入取值有限制
- 任意项:输入变量某些取值下,函数式为1/0不影响逻辑电路的功能
- 利用无关项化简函数
- 基于一定的物理背景下的应用(特定物理背景决定无关项有哪些)
- 利用卡诺图化简时,对于没有圈进去的约束项,是作为0来对待的
- 卡诺图3变量标号:0132/4568
- 若逻辑式中的某些项与约束项重合,可能是因为没有确定的物理背景,表达不清晰。在计算中将相关的“1”用“x”替代
- 无关项
- 机器化简法
组合逻辑电路
注意:进行电路实验的时候,要接电源/接地
-
组合逻辑电路的特点
- 功能:任意时刻的输出仅仅取决于该时刻的输入
- 从电路结构上:不含记忆(存储)元件
- 在设计时,不存在环
-
功能描述
- 有一个或多个输入/一个或多个输出
- 输入输出之间的功能要描述清楚
- 时间性:在特定时间内完成相应运算
-
设计方法
- 逻辑抽象
- 分析因果关系,确定输入/输出变量
- 赋值
- 列真值表
- 写出函数式
- 选定器件类型
- 根据所选器件对逻辑式化简(门)/变换(MSI)/或者进行相应的描述(PLD)
- 画出逻辑电路图,下载到PLD
- 逻辑抽象
-
常用组合逻辑电路
-
编码器:将输入的高低电平信号转换为对应的二进制代码
- 普通编码器:任何时候只允许输入一个需要编码的电平信号
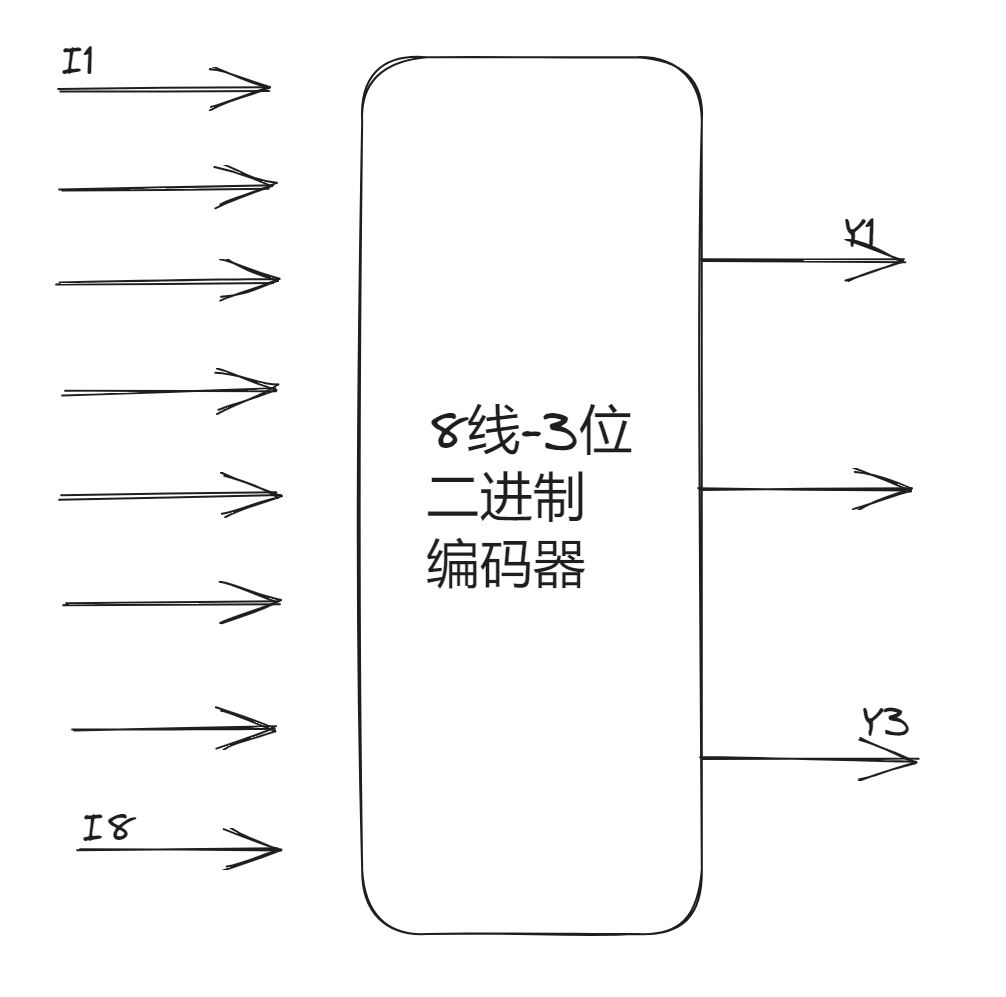
- 真值表示例:
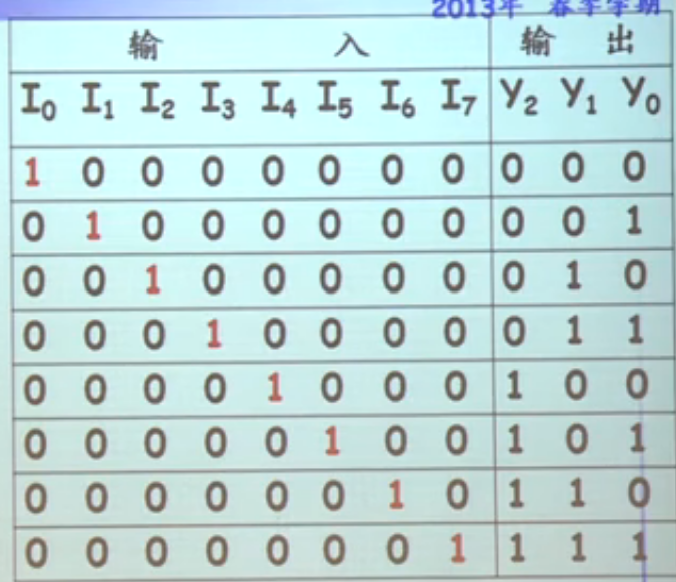
只列出了一部分,剩下的属于无关项中的约束项
- 利用无关项化简:;;
- 优先编码器:允许同时输入两个以上的电平信号,但只对其中优先权最高的一个进行编码
- 真值表示例:(仍然是8线3位)
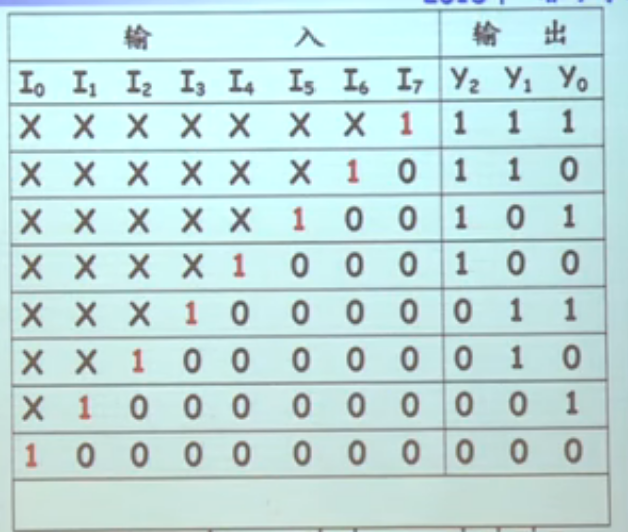
(这张不全,需要在下面加一行全为0的行,但这样又导致两个输出相同,出现了编码错误,所以需要再加一位)实例:74HC148(注意到这个图是低电平,也就是所有的输出都要取反)
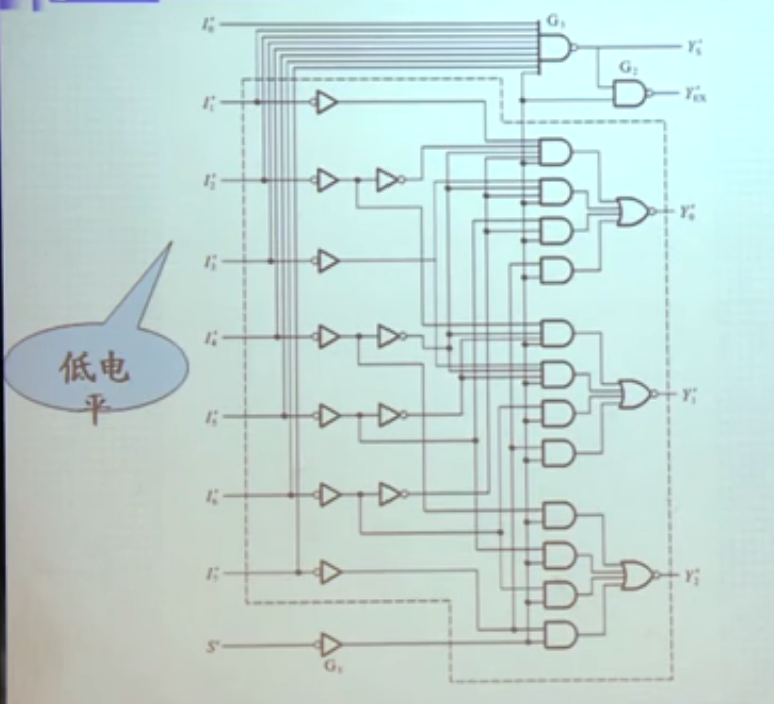
输入端多了S端(左下),输出端多了右上的两个端口;S端是选通端(select),考虑S后,公式变为:,S在这里有着类似“总开关”的作用。,,代表:电路允许运行,但没有输入信号;代表:电路允许工作,且有(至少一个)信号输入。示意图:
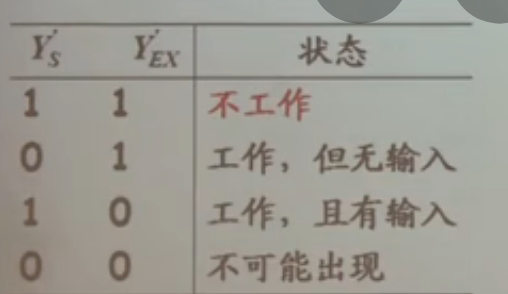
故而,加入上述几个输入输出端后,真值表变为:
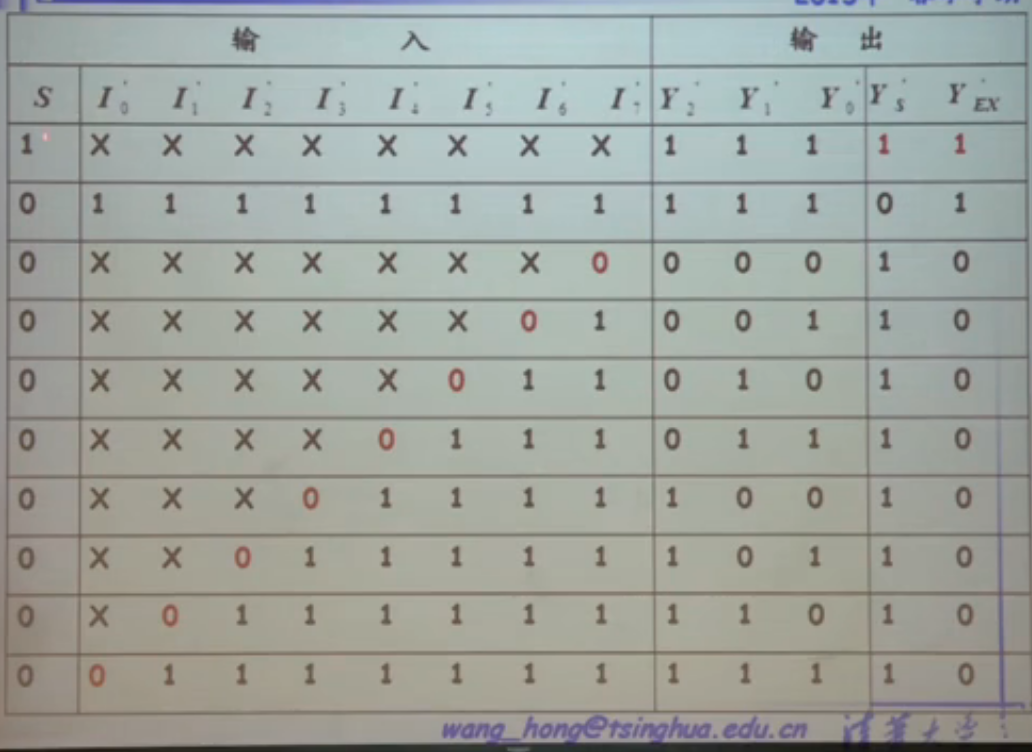
- 选通端的作用:将电路一级一级隔开,使得前端的电路对后端电路没有影响
- 公式化简:反复使用,得到,
- 如何用两个8-3编码器拼成16-4(其中的优先权最高)的编码器?
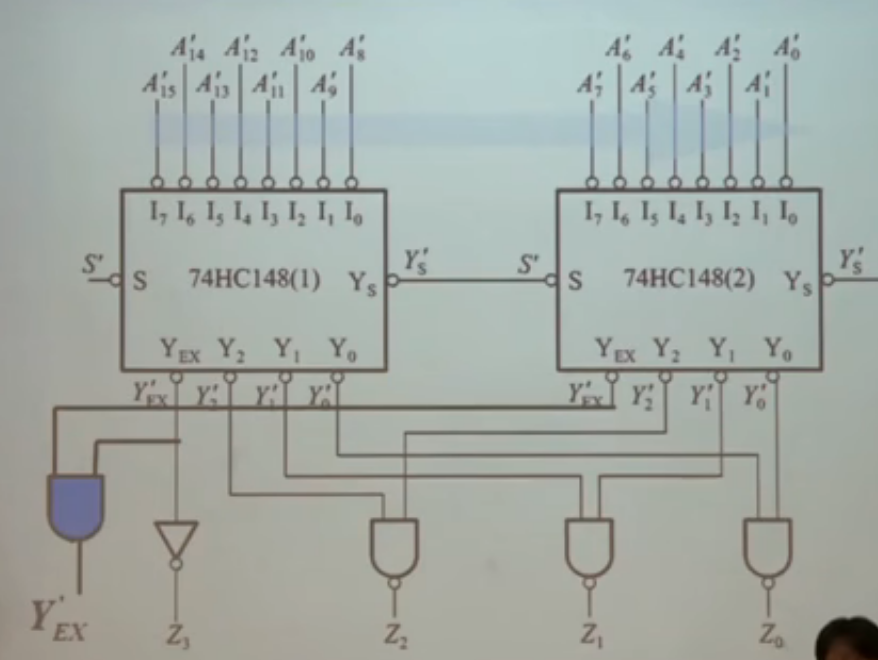 其中,端作为两个芯片的启动端,若接高电平,则两个芯片都无法工作。与直接连接,标志前一个芯片是否工作。注意,第一片芯片为高优先权;(1)编码输入时,(2)才允许工作;低三位输出是两片输出的“或”;仍然与8-3编码器中的功能相同。
其中,端作为两个芯片的启动端,若接高电平,则两个芯片都无法工作。与直接连接,标志前一个芯片是否工作。注意,第一片芯片为高优先权;(1)编码输入时,(2)才允许工作;低三位输出是两片输出的“或”;仍然与8-3编码器中的功能相同。 - 2-10进制有限编码器:10个输入(个值输入),但是由于的优先级大于,所以叠在一起,只有11行真值表。可以用剩下6个没用的编码中的一个表示“没有任何值输入”
- 普通编码器:任何时候只允许输入一个需要编码的电平信号
-
译码器
- 译码:将每个二进制编码转换为高低电平(狭义)
- 常用的译码器有:二进制译码器,二-十进制译码器,显示译码器等
- 二进制译码器
- 3-8译码器,经典实现:74HC138
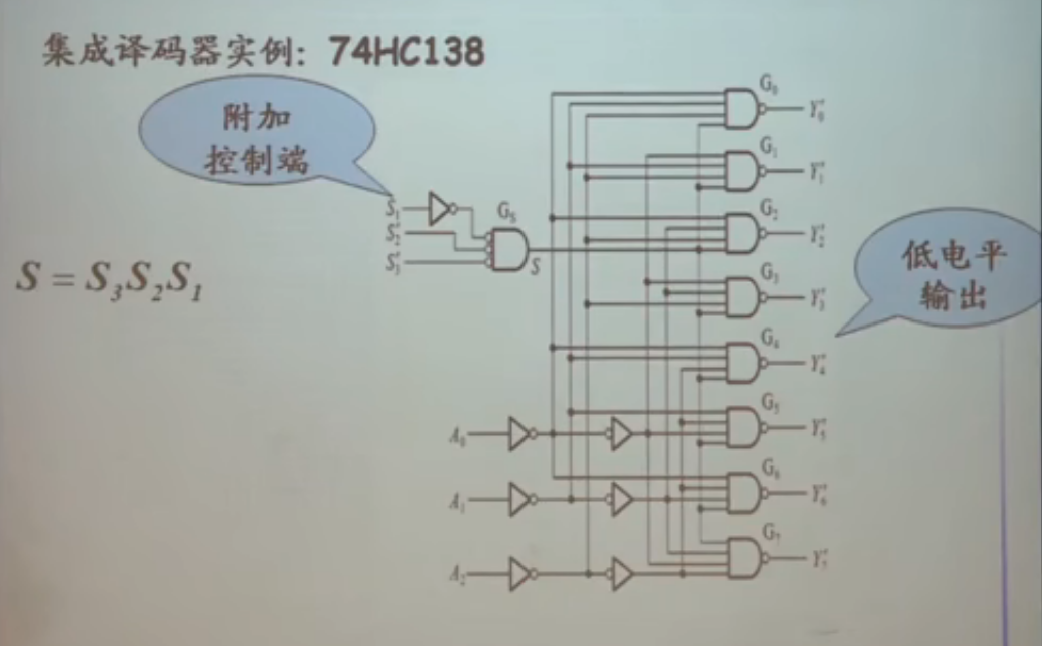
- 3-8译码器,经典实现:74HC138
附加控制端:前端控制端中:给高电平,、给低电平。
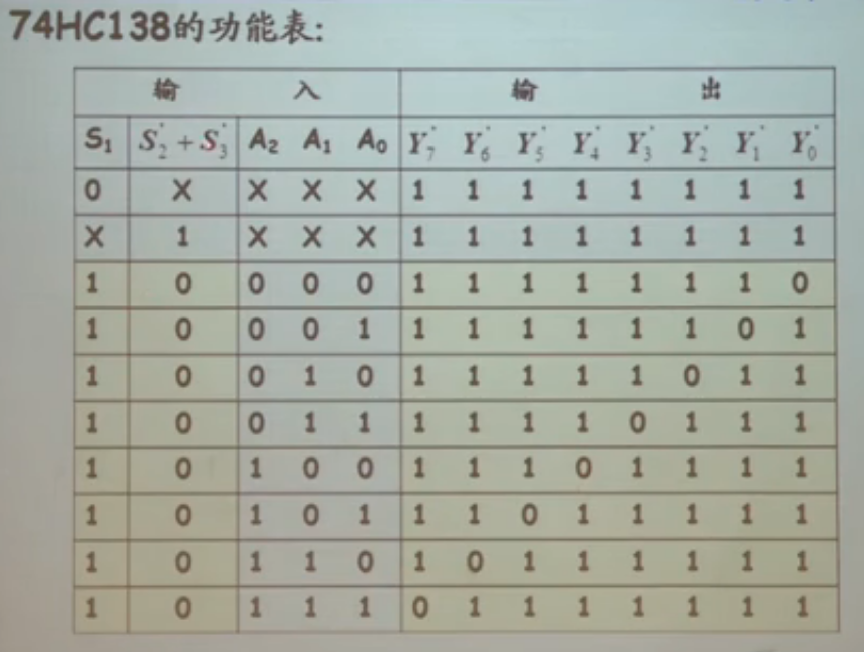
- 4-16译码器
- 示意图:
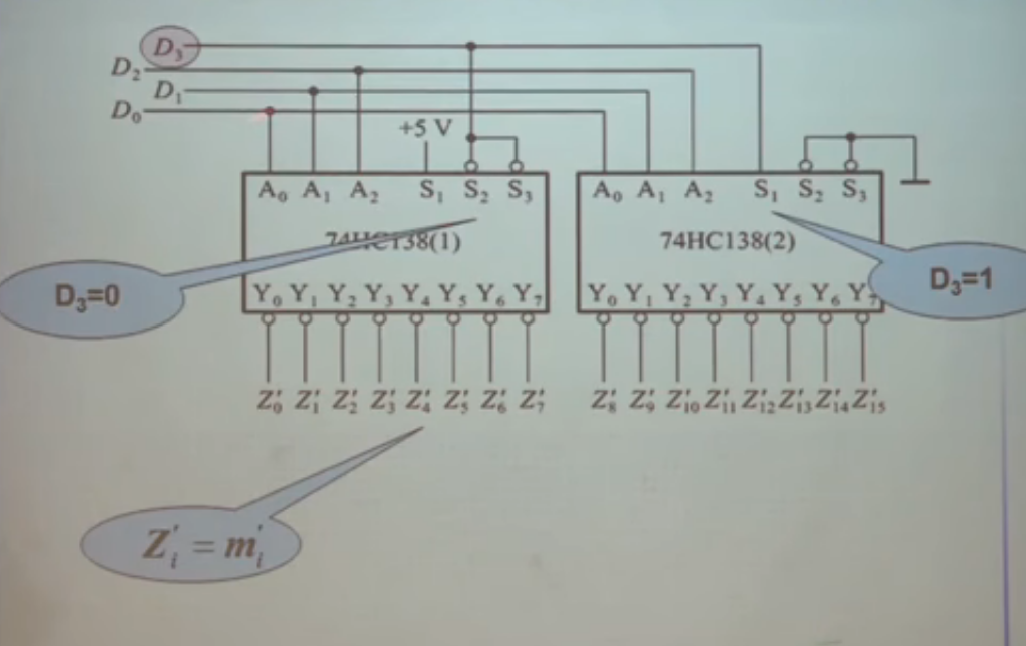
-
二-十进制译码器
- 输入4位,输出为一组十个电平
- 不存在化简的问题(一对一),所以不用考虑无关项
-
用译码器设计组合逻辑电路
- 原理:n位二进制译码器可以给出n变量的全部最小项。将n位二进制译码输出的最小项组合起来,可以获得任何形式的输入变量不大于n的组合函数。
- 方法:表达出最小项之后,再进行逻辑运算
-
显示译码器
- 七段字符显示器(7448)
- 附加控制信号
- 灯测试输入:当其为0时,~全部置为1
- 灭零输入:当所有输入都为0且其为0的时候,全部灭灯
- 灭灯输入/灭零输出(双极性工艺,既允许输入又允许输出)
- 灭灯输入控制端:,数码管熄灭
- 灭零输出端:,且灭零输入信号时,才给出低电平——表示译码器将原本应该显示的0熄灭了。
- 举例
- 附加控制信号
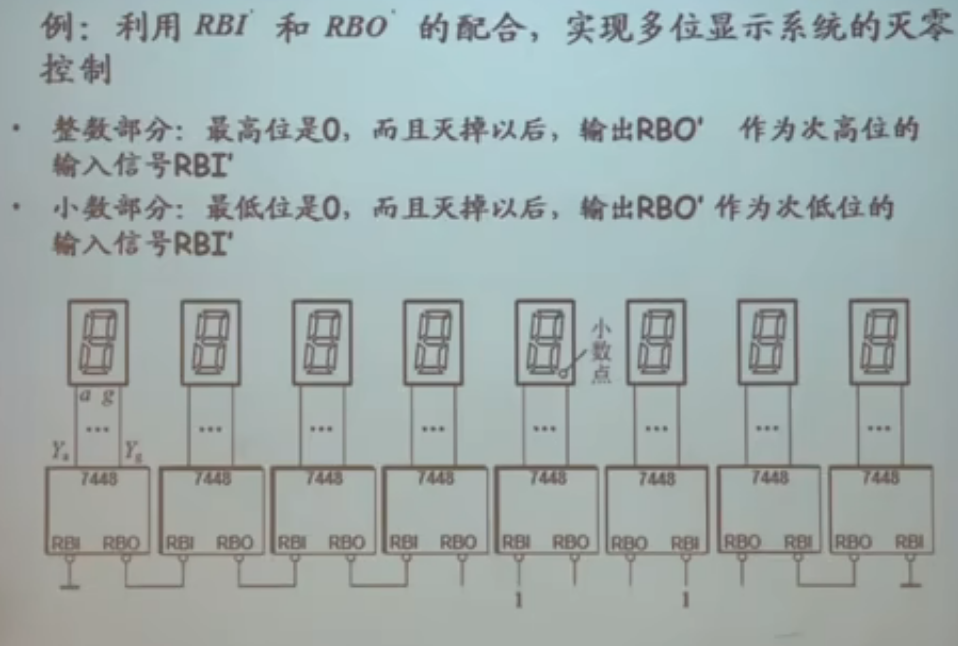
- MC14547,示意图:
- 七段字符显示器(7448)
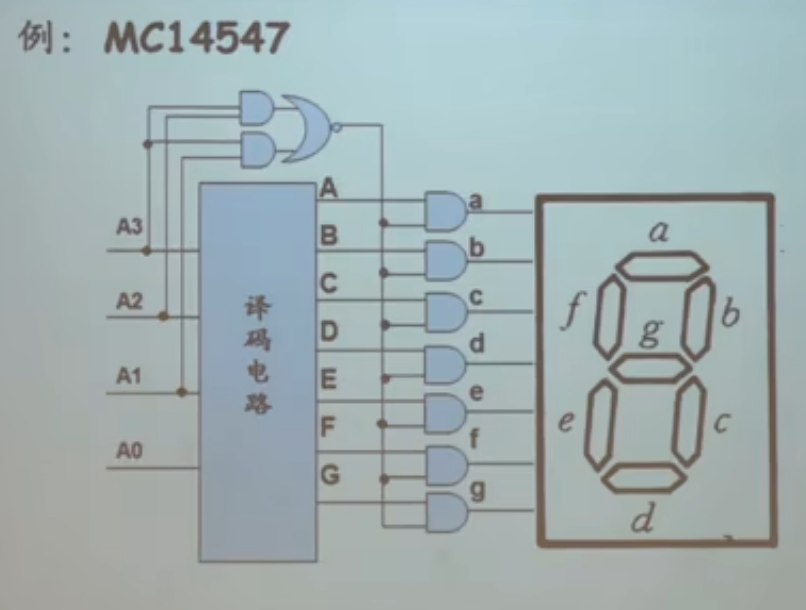
最上方的电路满足:10以上灭零
- 因为外围存在的电路,译码电路译出的10-16项没有意义——称为任意项
- 约束项和无关项与设计有着密切的联系
-
数据选择器
- 原理:通常以梯形的方式出现,相当于一个单刀双掷开关。待选数据位与选择位的关系:待选数据位=
- 使得电路可以与不同的来源相连
- 例子:74HC153,其中的S端是控制端(双四选一)
- 用四选一接成八选一
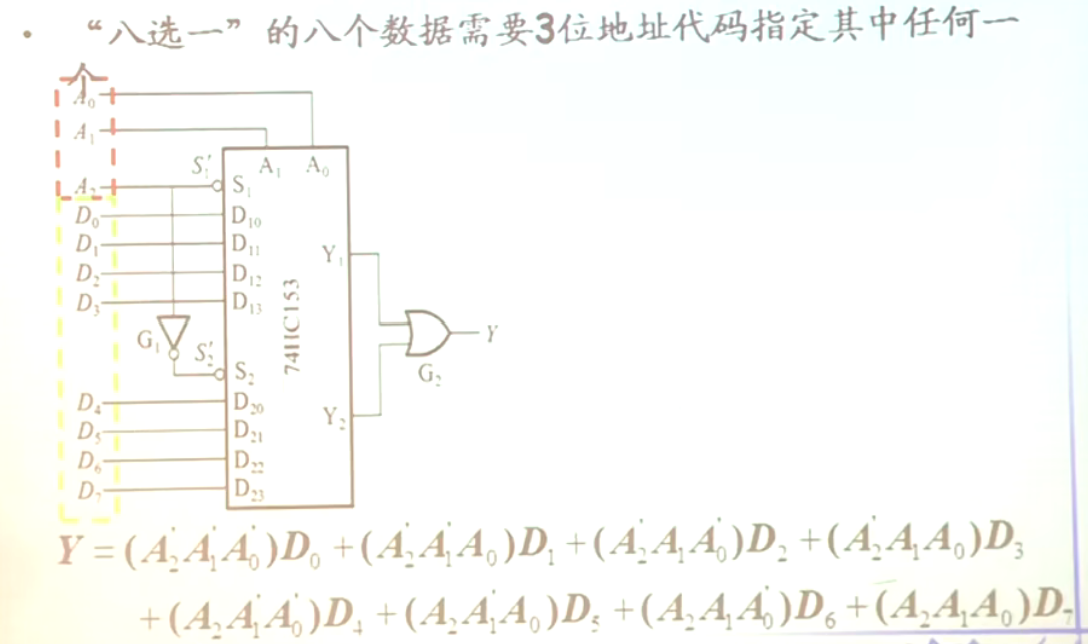
- 用数据选择器设计组合电路
- 基本原理:用数据选择器实现任意三变量的逻辑组合。若把接入第四个最小项,可以表达所有四变量的逻辑函数。因为可以通过接相反的电平来表示另一半变量。具有n位地址输入的数据选择器,至少可产生输出变量不大于n+1的组合函数
- 优势与缺陷:数据选择器直接输出和函数,搭建电路更方便;译码器可以复用最小项,而数据选择器不能。
- 加法器
- 半加器:不考虑�来自低位的进位,将两个1位的二进制数相加

- 全加器:将两个1位二进制数及来自低位的进位相加
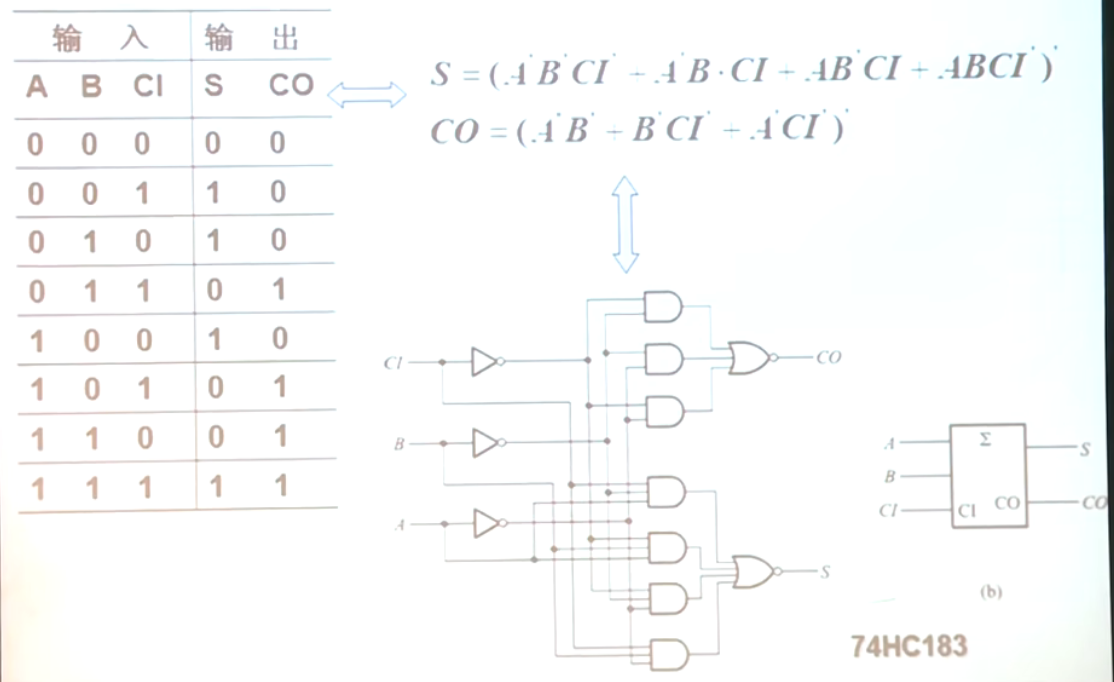
- 多位加法器
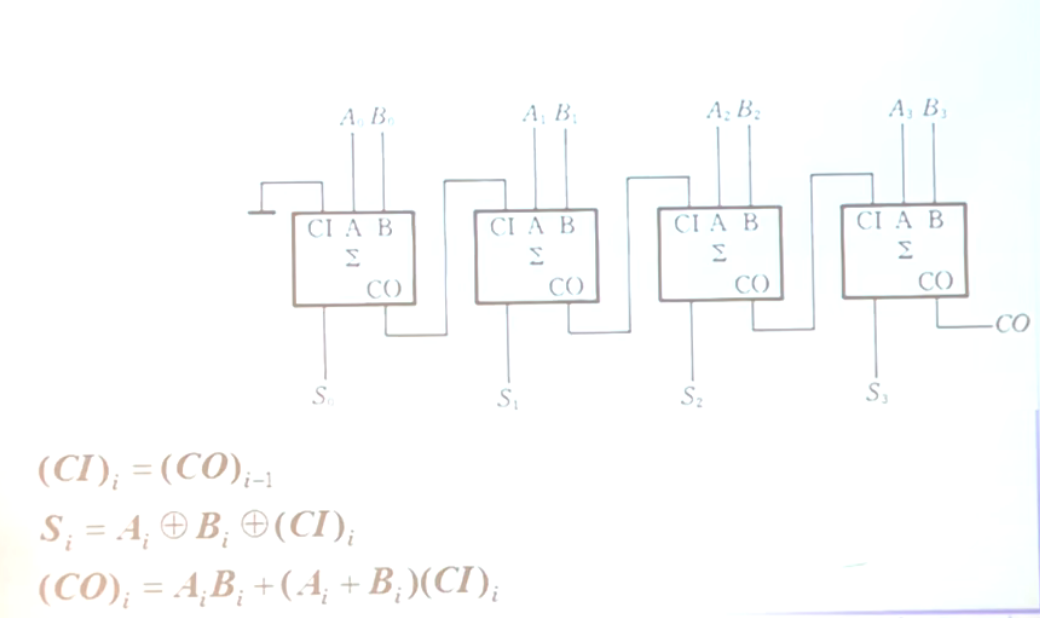
优点:复用性好;缺点:传输延迟时间()较长,导致信号发出后,需要等一段时间才能得到可信的信号;无效延迟时间()较短,导致输入信号变化后,输出的信号很快就不可信了,不能采用。改掉缺点的方法:不使用代入定理,而是将相关的逻辑式直接输入,用门电路连接之。(超前运算加法器代表:74HC283)这样做的缺点是使得电路规模大大增大且复用性差,但是速度快了许多。 ^0975c2
- 用加法器设计组合电路——输入变量输入变量相加/输入变量和常量相加
- 乘法器
- 数值比较器
- 1位数值比较器
- 74HC85比较四位
-
-
问题:在输入信号发生变化时,输出的数据有可能是无效的(考虑传输延迟时间与无效延迟时间)
- 解决:CMOS工艺确保组合逻辑电路具备一定的容差能力:如果输入信号中的一个信号可以确保输出值,那么另一个信号的变化不会对输出值的值造成影响(但是,从真值表的一行跳到另一行仍然会造成无效数据的产生。
-
组合电路中的竞争-冒险现象
-
竞争:两个输入同时向相反的逻辑电平变化,考虑传输延迟时间,出现了一个尖峰,称为“竞争-冒险”
-
检查方法
- 分析:输出函数一定情况下可以整理为:或者(其他输入变量固定,变为存在一个传输延迟时间,造成尖峰的产生)
- 观测:仿真或者实际电路
-
消除方法
- 接入滤波电容
- 引入选通脉冲(过一段时间之后,再输出)
- 修改逻辑设计
- ,在的情况下,存在竞争-冒险
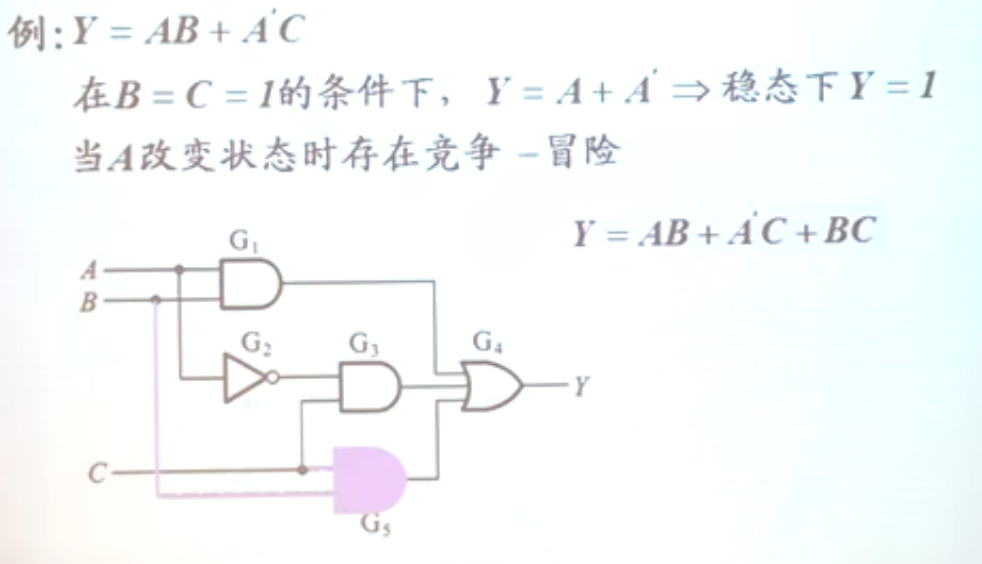
- 卡诺图相切,一定存在固定的竞争冒险,消除的方法就是圈住相切的元素,并且将其组合加入卡诺图之中
-
-
PLD:可编程逻辑器件(programmable logic device)。一种按通用器件生产,但逻辑功能是由用户通过对器件编程来设定的
-
PLD是一种电子面包板,通过综合(把电路的描述作为电路的实现)连接器件
-
FPGA芯片
-
EDA(Electronic Design Automation)电子产品从设计、仿真调试、硬件实现全过程自动化 ^5ac042
- 以超大规模的IC为基础,以高性能计算机及软件为平台
- 电路软件化:软件即是电路/用计算机程序描述电路
- 电路的描述形式:HDL Hardware Description Language
- 描述电路的连接
- 描述电路的功能
- 在不同抽象级上描述电路
- 描述电路的时序
- 表达具有并行性
-
两种语言:Verilog&VHDL
- VHDL侧重于系统级描述——系统级设计
- Verilog侧重于电路级描述——电路级设计
触发器:电路结构带来的性能变化
同步信号与时钟触发有关的信号称为同步信号。与时钟触发无关的信号称为异步信号。
- 难点:设计一个与电路过去状态相关的电路
- 出现了“状态”,需要记录电路过去的状态
- 出现了“事件”,输出由“输入”这个事件而非“输入值”决定。
- 解决:需要记录电路过去的状态——时序电路;同时对相关逻辑进行计算。其中,存储过去状态的数据时,要考虑传输延迟时间。
- 问题:需要一个存储的单元——用门电路构成
- 触发器:用来记忆1位二进制信号
- 有两个能自行保持的状态
- 根据输入信号,置成0或1
- 触发器的分类
- 触发方式:电平、脉冲、边沿
- 按逻辑功能:RS、JK、D、T
- 两个部分共同组成对触发器的描述。
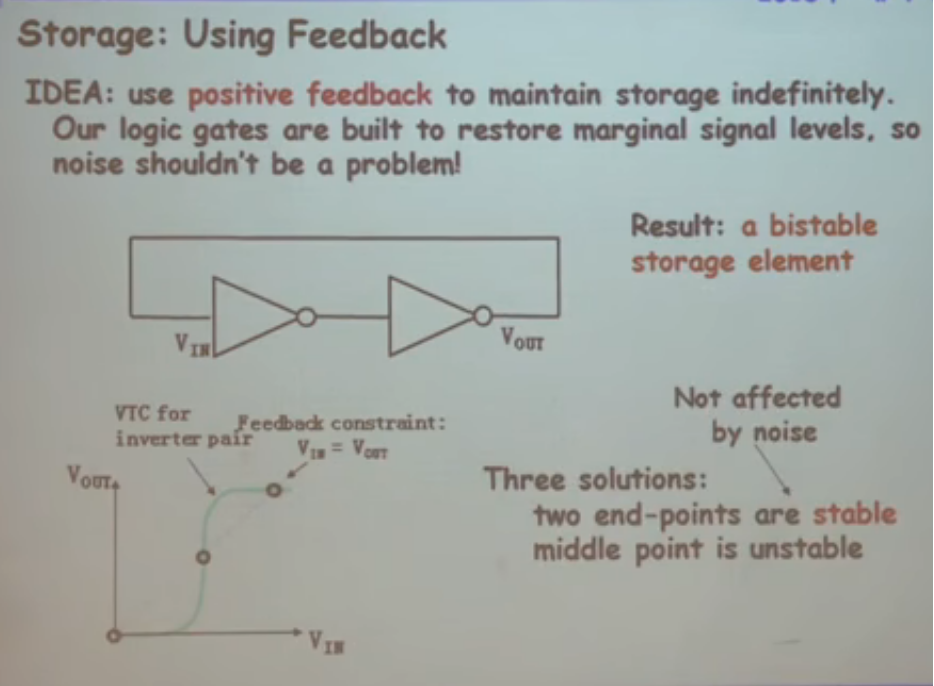
- 利用反馈存储-SR锁存器
-
示意图
-
分析:有两个自行保持的状态;但不能根据输入信号置成0/1
-
改进:利用或非门(与非门也可以)
-
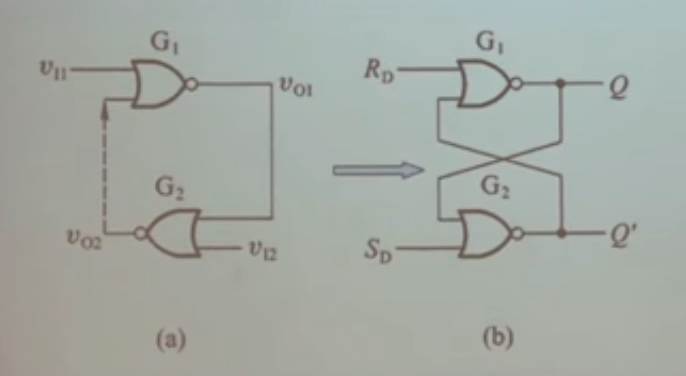
如果把置为,置为,那么输出为,输出为,之后把与都置为,就可以储存了。如果将、的值反过来,之后仍把两个值都置为,就可以储存了。
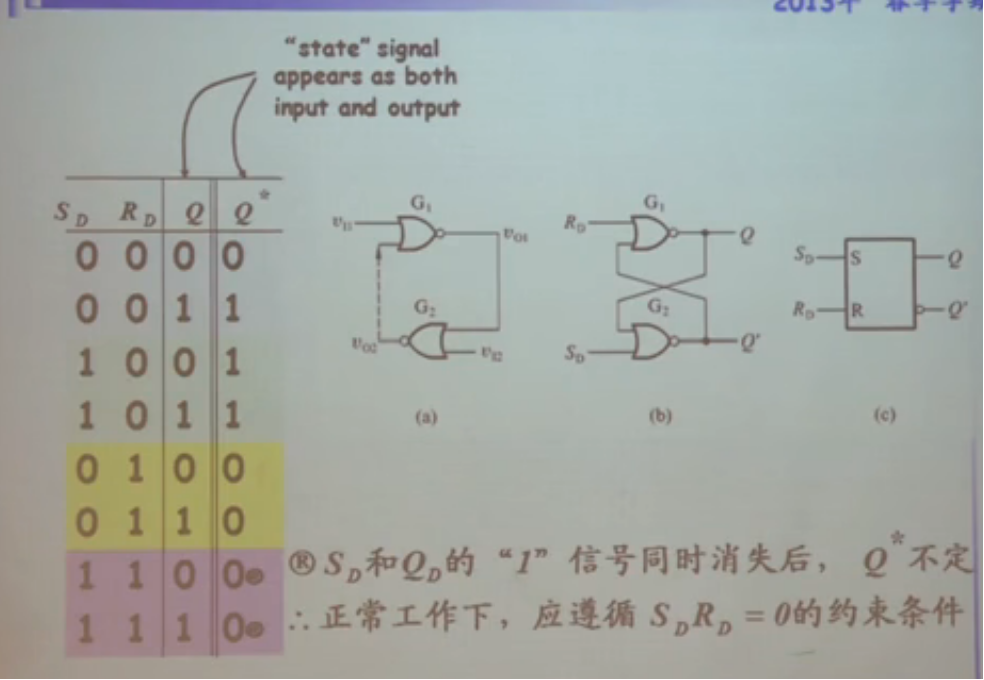
- 之后封装。
- 若拿到这个封装器件时,与都为,则说明器件保存了上个时刻输入的状态
-
动作特点:在任何时刻,输入都能直接改变输出的状态。
-
问题:外界电路的风吹草动都会对该电路造成影响。需要一个Load信号来调节何时输入。
-
解决:电平触发的触发器
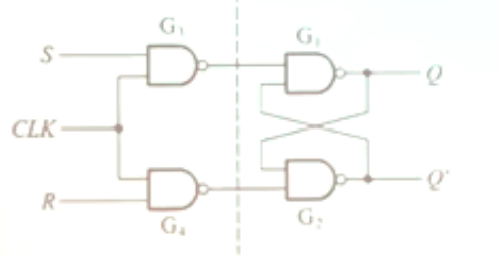 为时,方可输入数据。真值表为:
为时,方可输入数据。真值表为: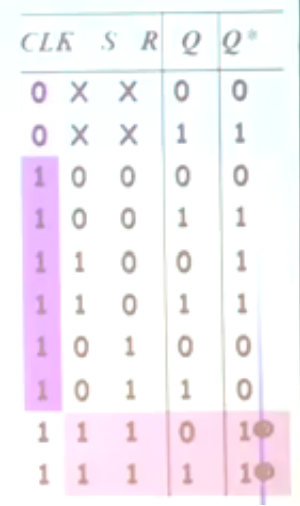
-
封装后:标号“1”的含义:先触发,触发之后才可能会有输入。
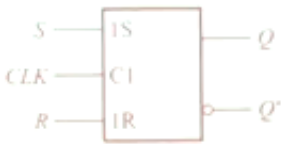
- 动作特点:在的全部时间里,与的变化都将引起输出状态的变化。
- 增加了两个新的端口:与是异步的端口,可以直接控制调或者调。
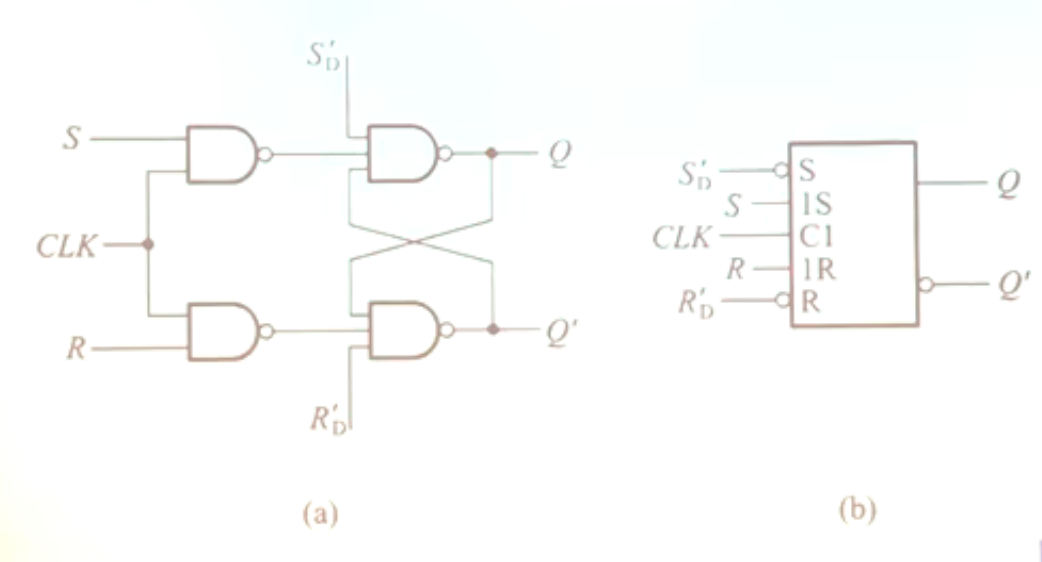
- 然而,此时仍存在“写数据的人脑子一热写错的问题”,而且,同时置一会造成错误。所以就有了D触发器:
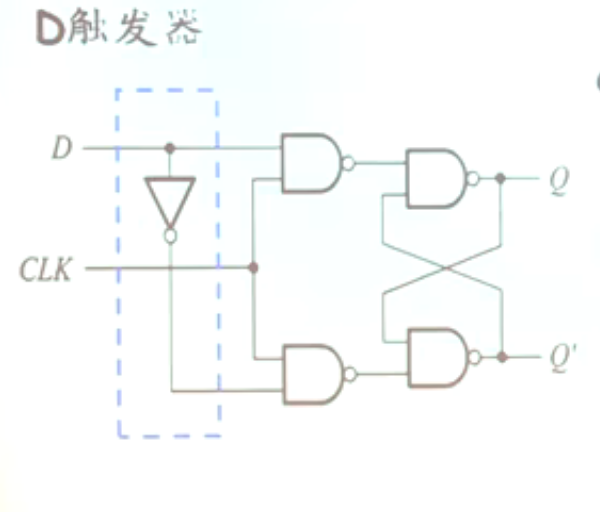
可以直接在D口处写入1或者0。问题:不具备两口均为0时保持元数据不变的功能。要实现相同的功能,只能不触发或者触发后不断写入。优点:永远知道下一时刻输出的值是什么。
- 另一种D触发器:
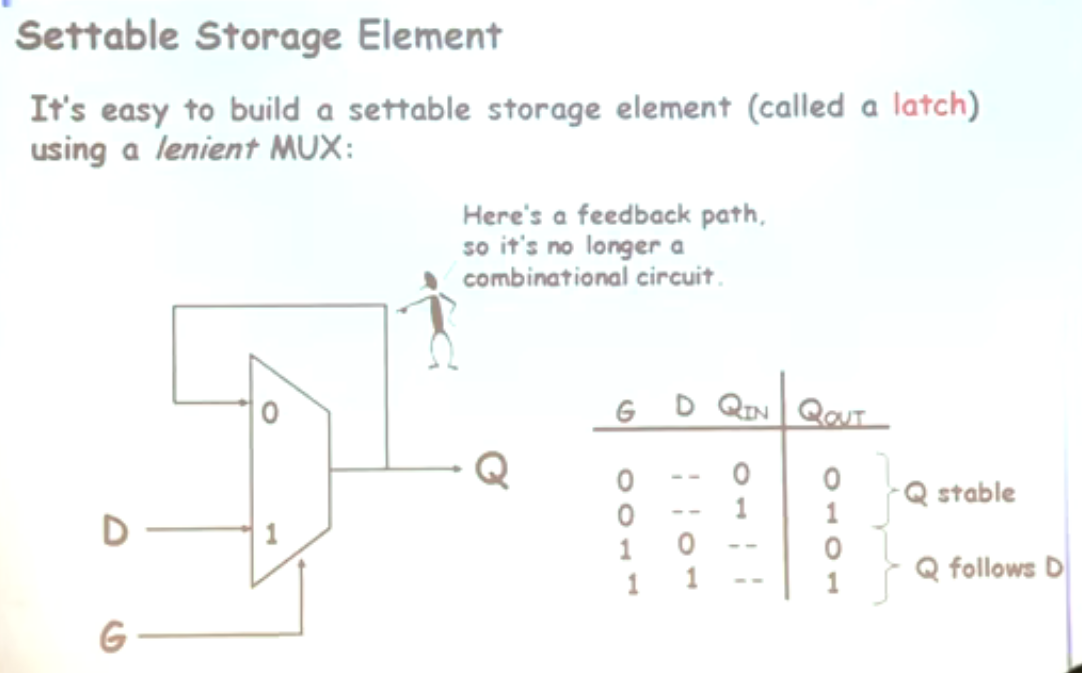
- 问题:若用D作为电灯开关的一部分,会出现问题。Load信号的长短会使得灯光闪亮。应当仅仅考虑“变化”对电路的影响,而不是“变化”的长度。
- 解决:脉冲触发的触发器(Edge-triggered,Master-Slave Flip Flop)
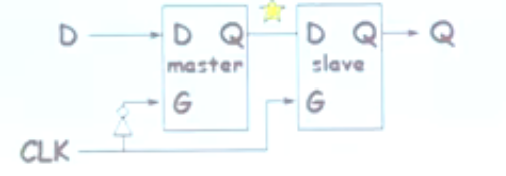
- Q只在从0到1变化时发生变化
- RS触发器也可以做成类似的样子。动作特点:在从1到0的时候发生变化
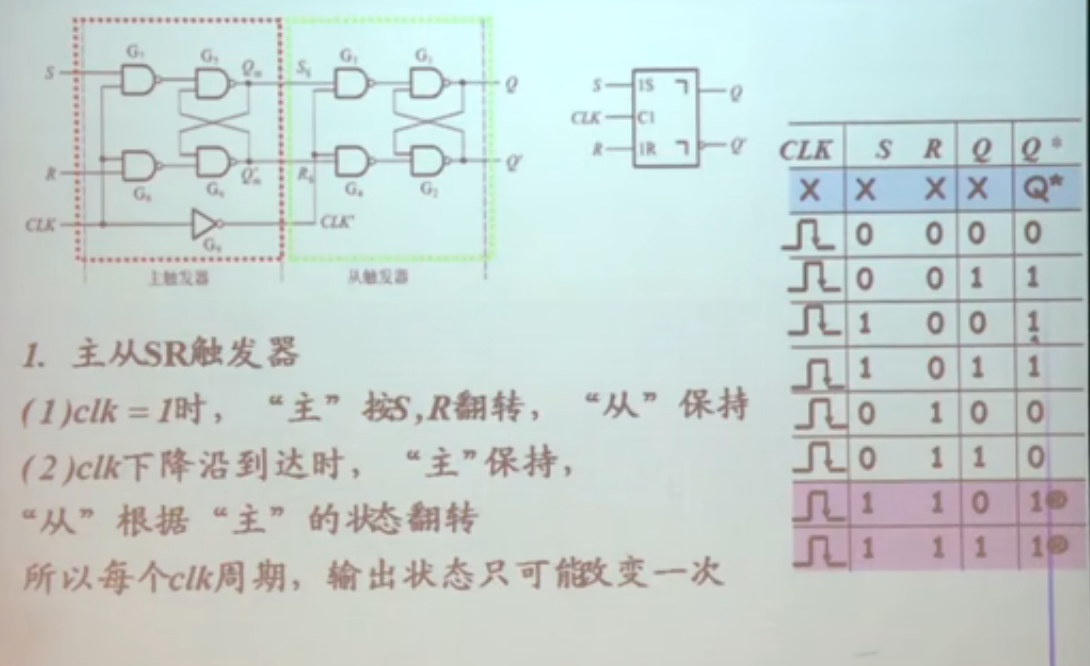
问题:如果在时间边沿到来之前,主触发器的输入端发生了瞬时变化,会对后面造成影响。因为SR触发器有保存效应,如果在时间边沿到来之前产生变化,那么SR的输出可能是新值,也可能是原来的旧值。而D触发器就不存在这个问题:因为D触发器的值是实时变化的。
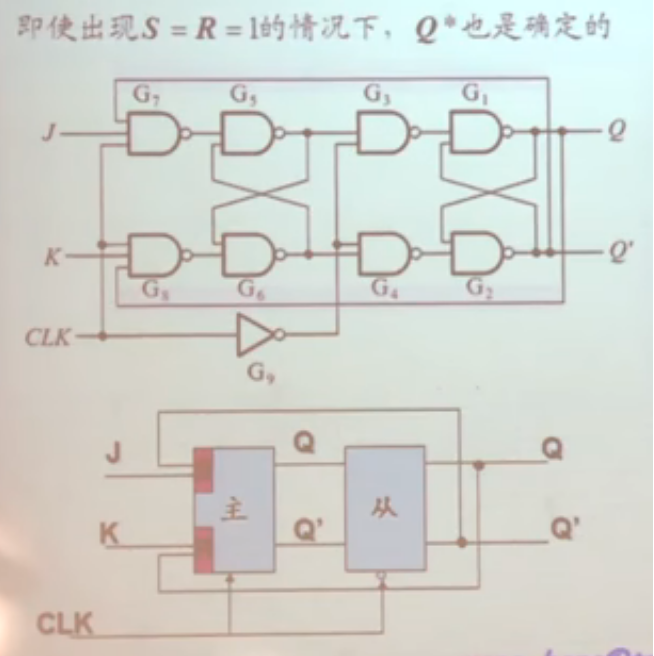
- 解决这个问题: 另一种解除约束(允许上述几种电路状态均出现,且不会对电路的输出造成影响)的方法:JK触发器
-
当clk=1时
- J=1,K=0:置一
- J=0,K=1:置零
- J=K=0:保持
- J=K=1:取反从
-
问题:在主触发器为1的情况下(也即,主触发器打开,且从触发器未打开的情况下,也就是前半周期),只能取反一次。因为出现了反馈电路,而反馈电路的值来源于从触发器的输出值。
-
触发器的动作特点:
- 第一步clk=1时,“主”触发器接受信号,“从”触发器保持
- 第二步clk下降沿信号到达后,“从”触发器按照“主”触发器状态翻转。(注意,每一个周期内,输出状态只能改变一次)
-
若是主从SR触发器,则clk=1的全部时间里,输入信号都对“主”起控制作用。但主从JK在clk高电平期间,“主”触发器的值只能翻转一次。在clk=1期间里,输入发生变化时,要找出clk下降沿前Q最后的状态,来决定Q*。所以...JK触发器的抗屏蔽能力并不好...
-
希望获得一种边沿触发的触发器:触发器的次态仅仅取决于clk变动到来之时的输入信号状态,与前后输入的状态没有关系。啊前面讲过了,俩D触发器放在一起,可以获得边沿触发器
-
【这里有一个CMOS门的bulabula没学过模电跳过了】
-
触发器的逻辑功能及表述方法
- SR触发器
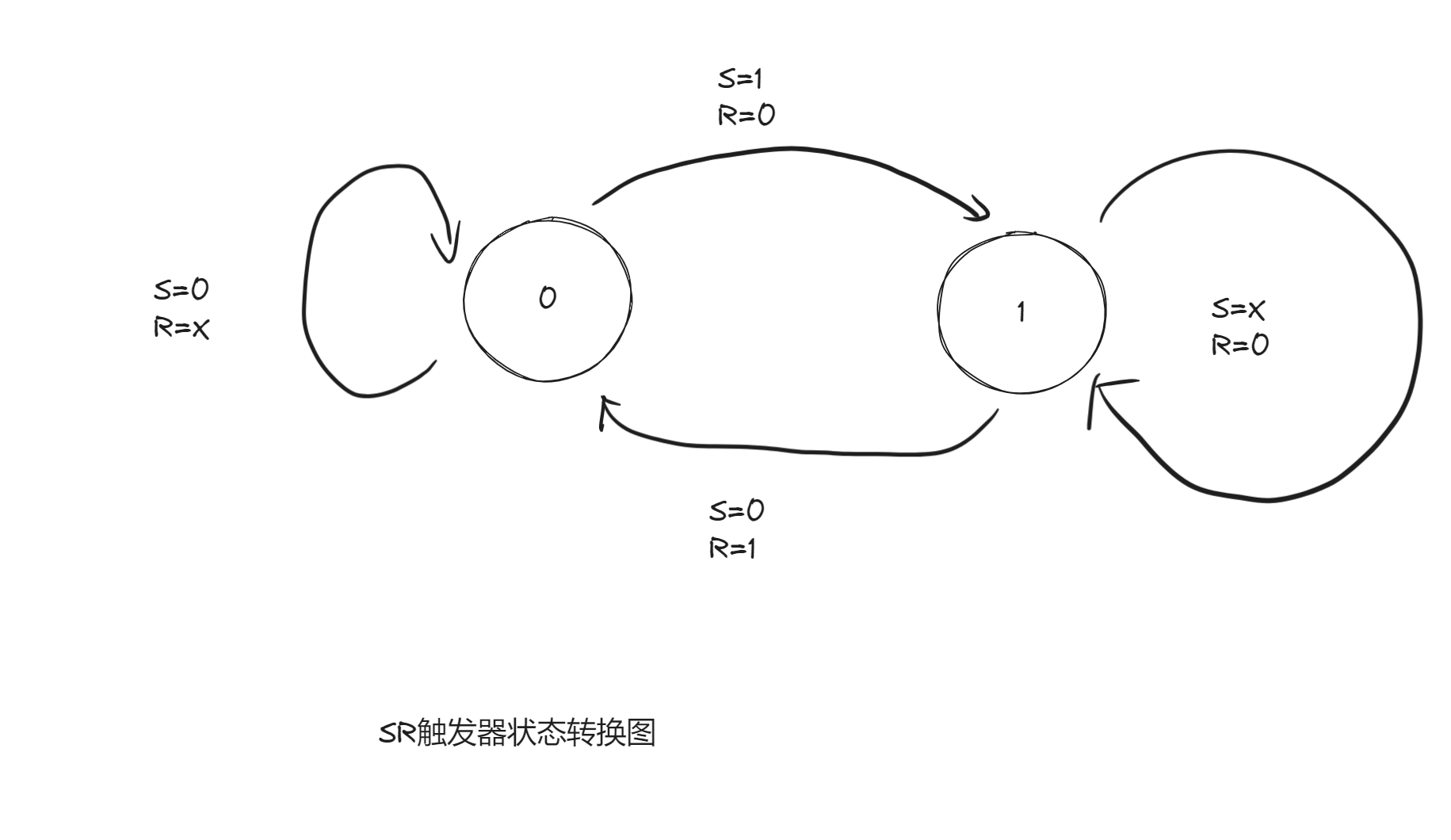
- 特性方程(右侧算式包含了所有为1的情况,而左侧只包含了其确定为1 的情况),约束条件:
- 状态转换图:
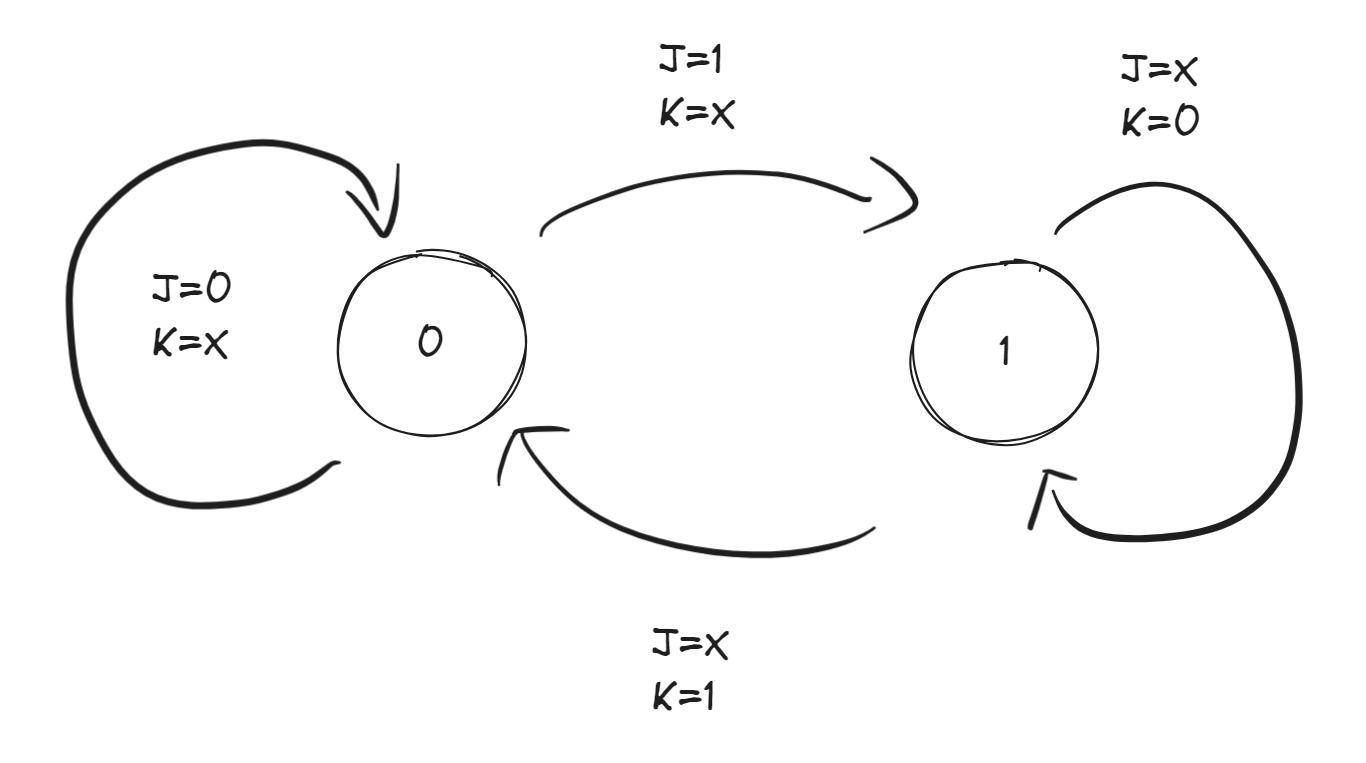
- JK触发器
- 特性方程:
- 状态转换图:
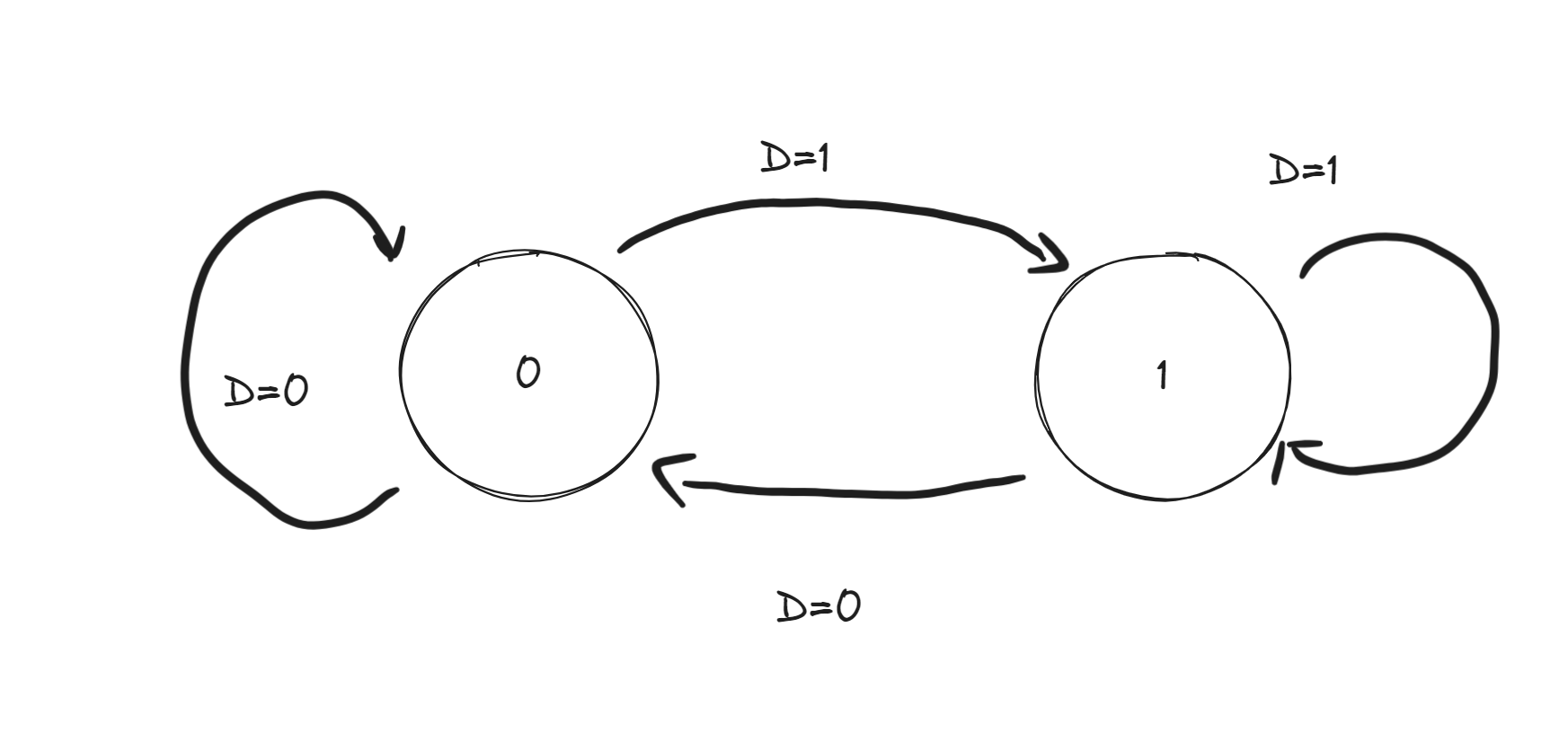
- T触发器 ^ea7c9f
- 特性方程:
- 状态转换图:
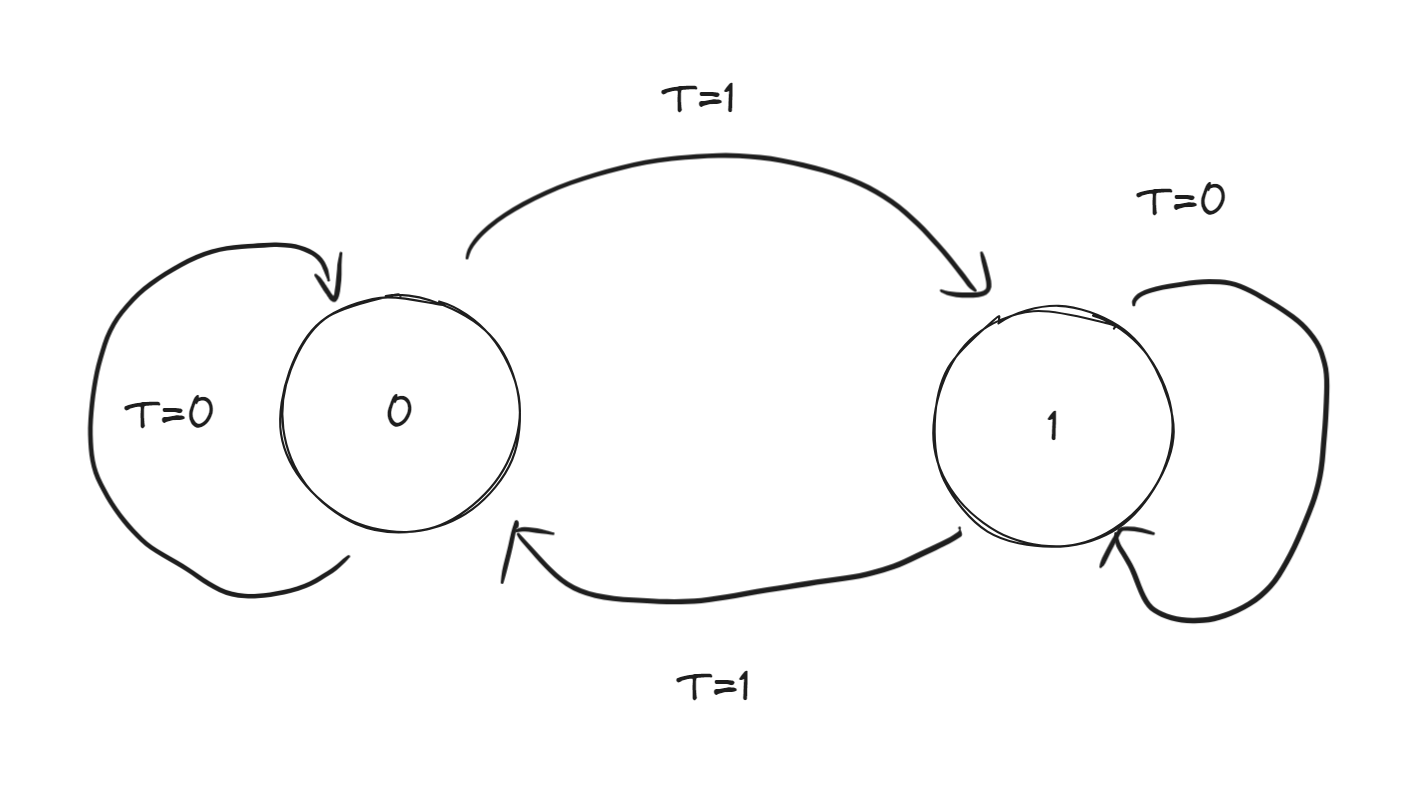
- 可以作为计数器,计数clk的个数(当t=1)
- D触发器
- 特性方程
- 状态转换图:
- SR触发器
-
触发器的动态特性
- 增加时间特性参数:描述数据信号与触发信号之间的配合(数据信号早来晚走,保证数据信号可以稳定地写入)
- 建立时间:在触发之前,把要写入的数据准备好
- 保持时间:触发信号到达之后,数据信号要保持一段时间
- 为什么要早来晚走?以电平触发的D触发器为例
- 写入数据并锁存的三个阶段
- ,的输入在一个中保持稳定
- 由1变成0,经过无效区,此时要且二者输入在一个中保持稳定
- ,输入在一个中保持稳定
- 结论:,不能同时输入,所以需要
- 首先输入数据,之后保持
- 在一个之后,信号输出,
- 在一个之后,与都表示出了欲输出的数据,不论此时输入数据是什么,都可以保证输出数据是
- 把置为0,一个之后,和二者共同使数据存入锁存器中。
- 综上所述:
- 也即,的值由1变为0时时,需要至少保持稳定这样的时间。
- 也即,在的值变化之后,输入的值需要保持稳定的时间
- 注意:这两个时间都是上限,目的是确保输出的值不出现问题。真实值需要在实验中发现。在边沿触发器中,clk的变化相当于信号的触发。此时在边沿之前。
- 写入数据并锁存的三个阶段
- 切换为主从触发器:从触发器也要满足上述“早来晚走”的规律。考虑主触发器的,发现此处必须满足,方可满足上述规律。如果不满足,可以加非门人为延长之。
- 总结:时间特性参数
- 信号带来的传输延迟
- :最大传输延迟时间
- :最小无效延迟时间
- 稳定工作的参数配合要求
- 信号带来的传输延迟
- 最高工作频率:两次触发的间隔
- 增加时间特性参数:描述数据信号与触发信号之间的配合(数据信号早来晚走,保证数据信号可以稳定地写入)
时序逻辑电路
概述
特点
- 任意时刻的输出不仅取决于该时刻的输入,还与电路原来的状态有关。
- 例子:把4位的全加器改成串行加法器
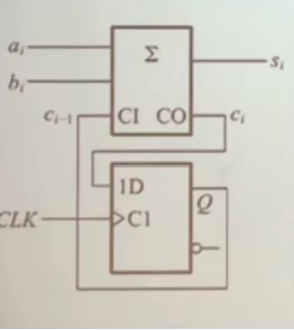
- 例子:把4位的全加器改成串行加法器
- 电路结构
- 包含存储电路和组合电路
- 存储器状态和输入变量共同决定输出
- 缺点:传输延迟时间变长,需要储存每一位的数据之后再并行输出
- 优点:可以进行位的输入
一般结构形式与 功能描述方法
- 方程组描述
- 输出(数据)方程
- 驱动(对输出的数据进行处理)方程
- 状态方程
- 只有一组方程与存储电路有关
时序电路的分类
同步与异步
- 同步时序电路
- 存储电路中所有触发器的时钟使用统一的clk,状态变化发生在同一时刻
- 优点:好分析
- 缺点:功耗比较大
- 异步时序电路
- 没有统一的clk,触发器状态的变化有先有后
- 优点:功耗较小
- 缺点:难以分析
- 应用:局部同步电路,大部分的电路会错开
Mealy型和Moore型
- Mealy型:
- 输出直接与输入有关
- 输入和时钟不同步,那么输出也与时钟不同步
- Moore型:
- 有输入,但是输出与之无关。
- 输出与clk有关
时序电路的分析方法(同步时序电路 )
- 目的:找出给定时序电路的逻辑功能。
- 步骤
- 从给定电路写出存储电路中每个触发器的驱动方程,得到整个电路的驱动方程
- 将驱动方程代入触发器的特性方程,得到状态方程
- 从给定电路给出输出方程
- 注意:列输出方程与驱动方程的时候不需要深究触发器相关的过程。这是状态方程需要考虑的问题。
- 之后画状态转换图/表 。注意避免真值表出现“锁死”状态。也即,无效态必须可以进入主循环。这样的电路称为“自启动”电路。设计电路的时候,尽可能使无效态变为初始态。
- 画状态转换图的时候:Moore电路要将输出画在输入的圈圈内,表示现态决定输出;Mealy电路要将输出写在两个圈圈之间的横线上,表示输出与时钟不同步,改变输入的同时出现输出。
- 例子
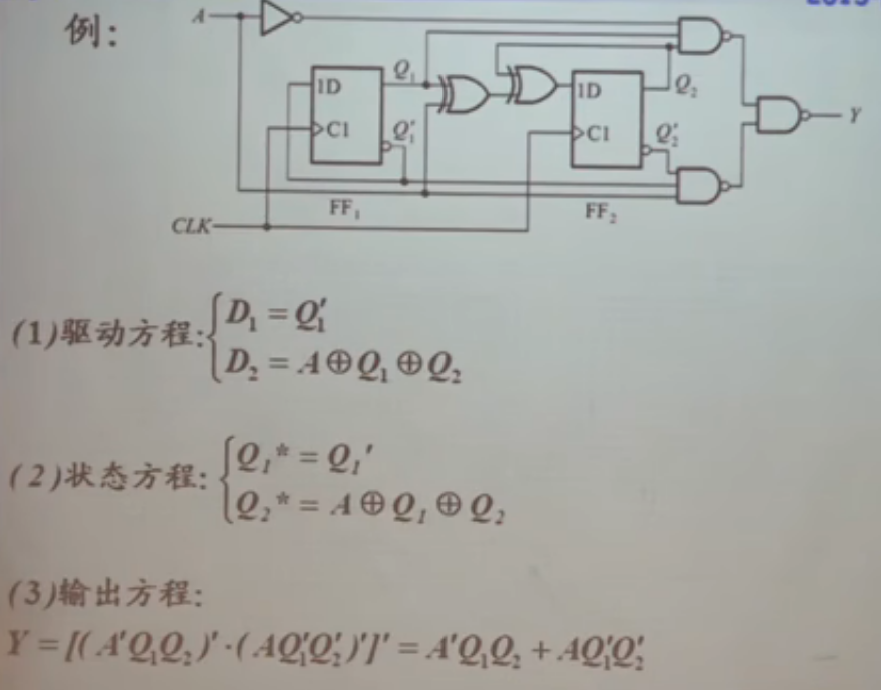
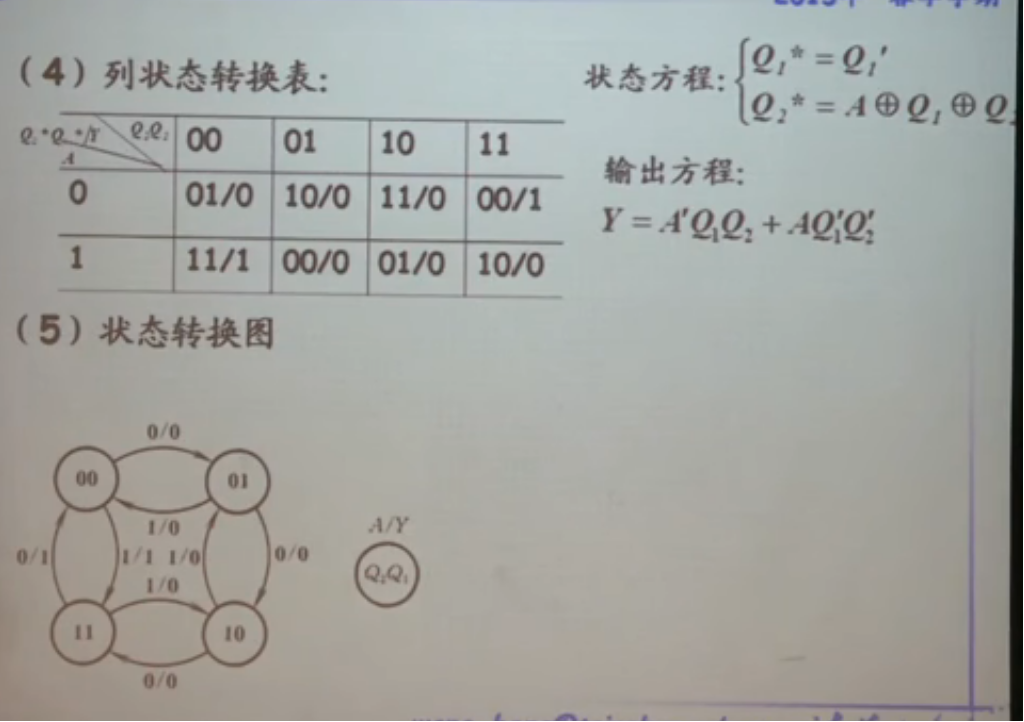 这个电路是可以自启动的。它的功能,是一个两位的二进制可逆计数器。代表加或者减;代表进位或者借��位。
这个电路是可以自启动的。它的功能,是一个两位的二进制可逆计数器。代表加或者减;代表进位或者借��位。
异步时序逻辑电路的分析方法
- 画波形图
- 考虑时钟
常用的时序电路
寄存器
- 用于寄存一组二值代码,位寄存器由个触发器组成,可存放一组位二值代码。
- 其中每个触发器可以置或置
移位寄存器
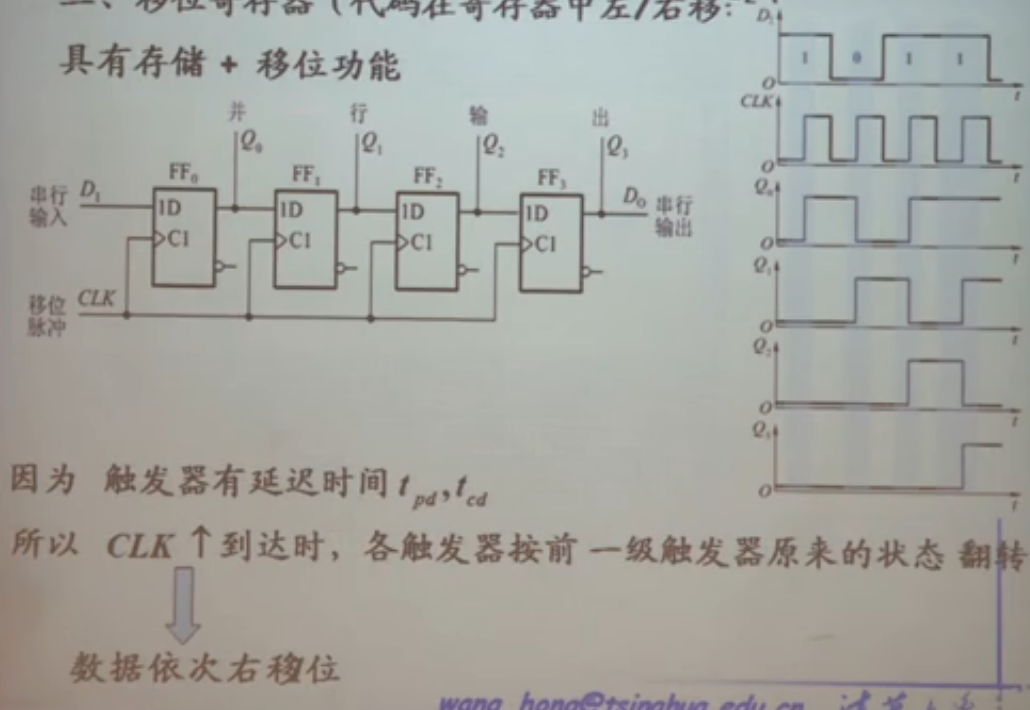 接在一堆连在一起的加法器上,来记录进位。
接在一堆连在一起的加法器上,来记录进位。
-
JK、RS都可以做移位寄存器。
-
电平触发不可以,因为不能作为节拍;主从触发:D,JK均可以,因为主从结构可以把数据拦住,并且JK触发器不会出现多次翻转的问题。
-
应用:
- 代码转换,串行并行输出,但不能反过来
- 数据运算
-
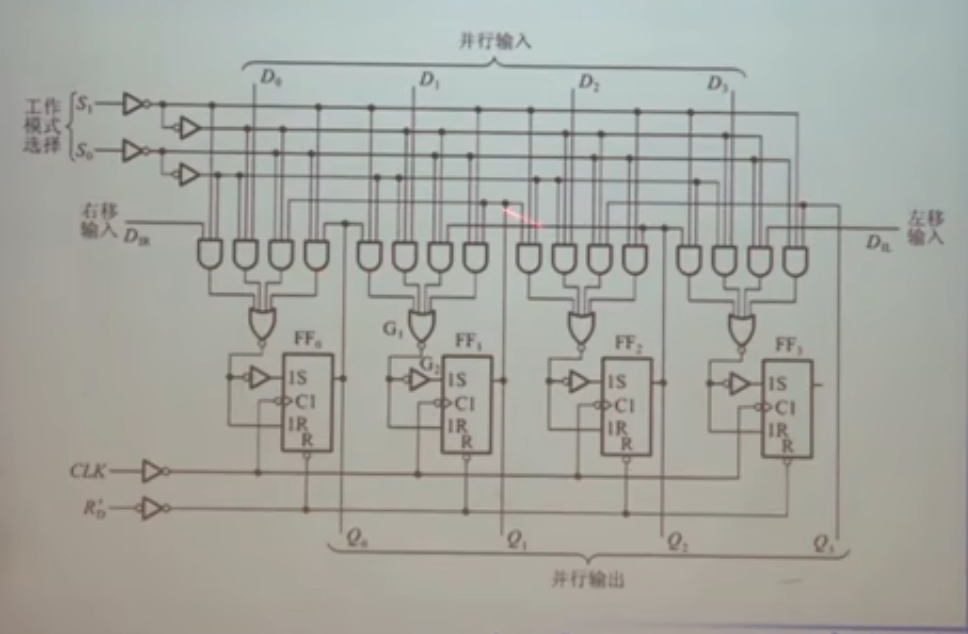
寻找一个寄存器,可以实现左/右移动,并行输入,保持,异步置零等功能
- 数据来源要有多种选择
- 任意时候只选择一个
- 综上所述:使用数据选择器
- 示意图
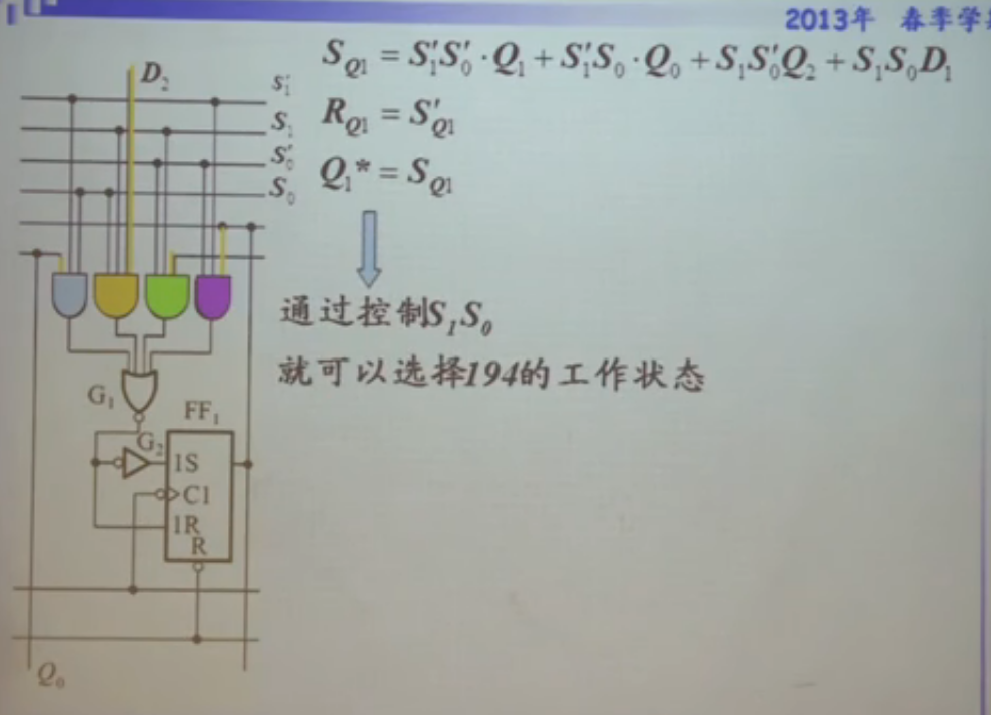
计数器
- 计数,分频,定时,产生节拍脉冲
同步二进制计数器
-
原理:在多位二进制数末位加1,若第i位以下皆为1时,则第i位应该翻转。
-
使用:T触发器
-
若用T触发器构成加法计数器,则第i位触发器输入端Ti的逻辑式应为:,(恒)
-
示意图
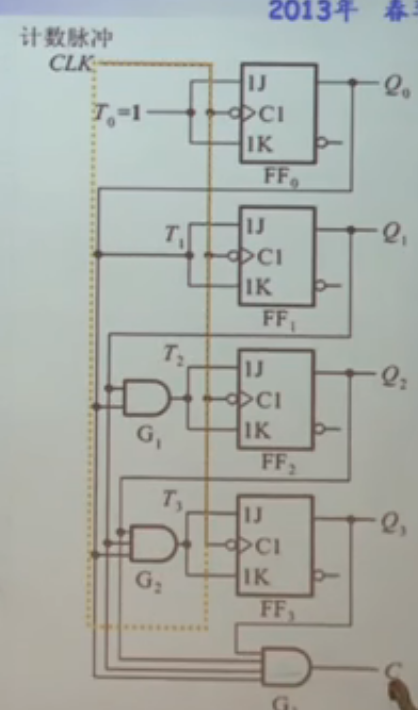
-
减法计数器 ,恒等于1
-
同步加减计数器
- 单时钟脉冲:加减脉冲共用同一输入端,由加减控制线的高低电平决定加减
- 双时钟脉冲:加减计数分别与两个时钟源相连,实现“伪同步”
同步十进制计数器
- 加法计数器:在四位二进制计数器基础上修改,当计到1001时,剩下一个clk电路状态回到0000
- 改动电路
- 无效态内不能形成循环
- 修改
- (前一项是二进制的规则,后一项是当变成1001时,下一步直接归零)
- 同理:
- 按照相同的思路,也可以改减法电路
异步计数器
二进制计数器
加法计数器
-
末位加1时,由低位到高位逐位进位
-
示意图
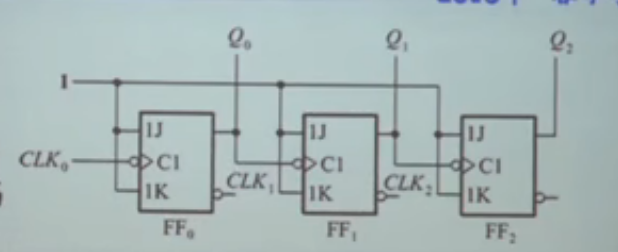
注意:如果从将输入端的取反都去掉,那么电路设计是错误的,因为变成了遇到1就翻
-
问题:由于每个触发器都会有一个,所以随着触发器的增多,这些累加起来,会变得越来越长,导致出现错误的组合,对电路的输出造成影响。
减法计数器
- 把上面图中的“圈圈”都去掉就可以啦
任意进制计数器
N进制芯片变成M进制计数器
-
:计数循环中设法跳过个状态
- 异步/同步置零法
- 异步/同步预置数法
-
若使用异步置零,则要在M+1个态时置零,M+1的态是暂态
-
使用同步置零,则在M态置零即可
-
进位信号要注意元件的具体性质...(啊懒得记了我就是懒得记了...)
-
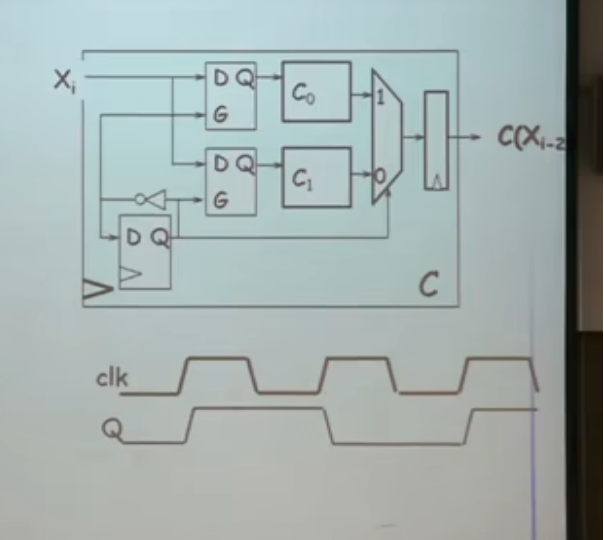
脉冲展宽电路
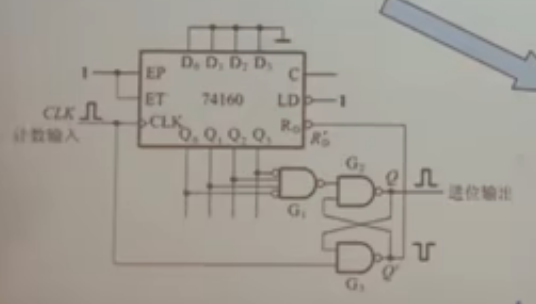 右下角SR触发器的上端是S端,输入信号为
当左边的输出为1时(此时clk恒为1),S端输入0,此时输出保持为。
当clk下降为0时,输出也降为
这个时候,一个窄脉冲就被展宽为半个clk的长度
右下角SR触发器的上端是S端,输入信号为
当左边的输出为1时(此时clk恒为1),S端输入0,此时输出保持为。
当clk下降为0时,输出也降为
这个时候,一个窄脉冲就被展宽为半个clk的长度 -
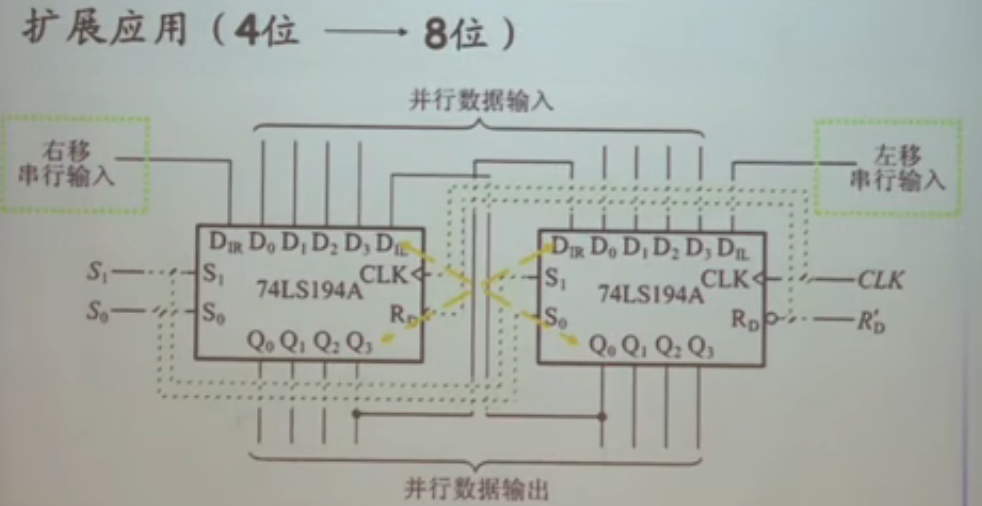
- 两种连接方式
- 并行进位:低位片的进位输出作为高位片的计数控制信号
- 串行进位方式:低位片的进位输出作为高位片的CLK,两片始终同时处于计数状态
- 不可分解,采用整体置零和整体置数法:先用两片接成的计数器,然后再采用置零或置数的方法。
计数器的应用
- 计数器+译码器=顺序节拍脉冲发生器
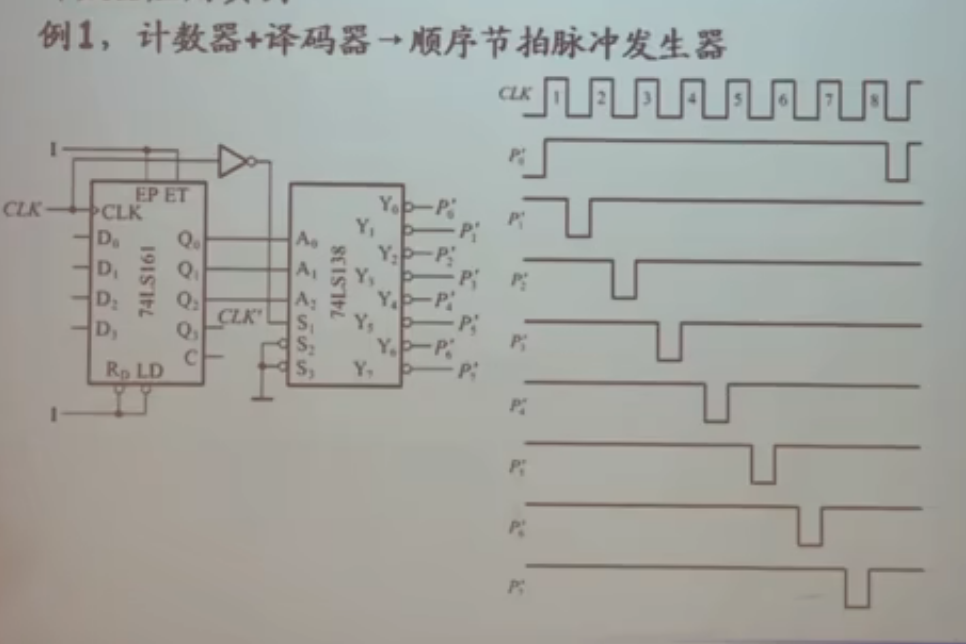
- 计数器+选择器=序列脉冲发生器
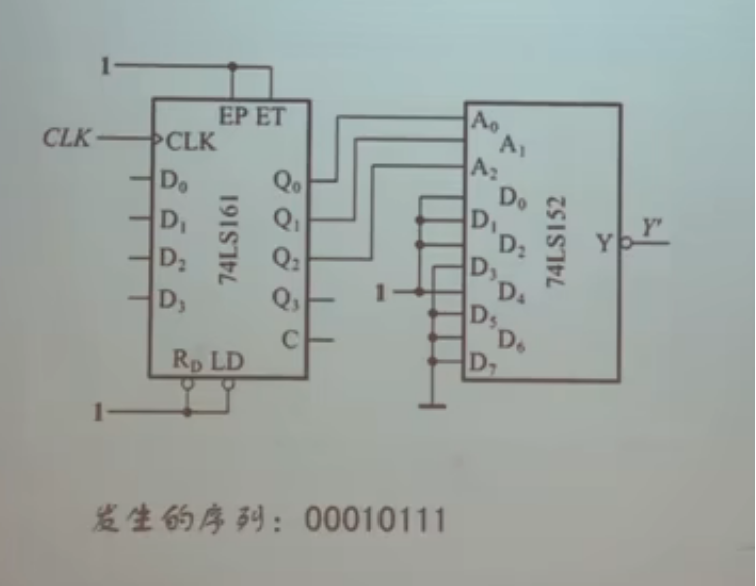
时序逻辑电路的设计方法
一般步骤
- 逻辑抽象:确定输入/输出,电路状态
- 定义相关的含义
- 列出状态转换表
- 画出逻辑图,检查自启动
- 状态化简:若两个状态在相同的输入下有相同的输出,并转换到同��一相同的状态,则称为等价状态,等价状态可以合并。
- 状态分配(编码)
- 确定触发器数目
- 每个状态规定一个代码
- 选定触发器类型
- 求状态方程,驱动方程,输出方程
设计时的注意事项
- 有关与
- 设电路中前后两个触发器分别为,,中间的逻辑电路为1。则有:,
- 若不满足,可以加进去东西,但是会导致时间频率的降低。
流水线
- 思想:利用触发器,尽可能提高组合电路效率
- 触发器放在输出,此时整个电路的吞吐量为;
- 传输延迟时间等于
- 目标:提高吞吐率
- 如何降低“花费时间最长的组合电路的时间”?
- 采用层次化设计,在电路的内部也使用流水线
- 最薄弱(时间最久的)的环节使用并行
- 左下角的是一个有限状态机,在0/1之间反复切换。在输出一个计算好的数的时候,另一个逻辑电路在计算。这样就提高了吞吐率。